Menu Close

If-lim-x-3-17-ax-3-1-3-b-x-3-136-27-then-8a-b-

Tinku Tara 0 Comments
Pin




Question Number 115027 by bemath last updated on 23/Sep/20
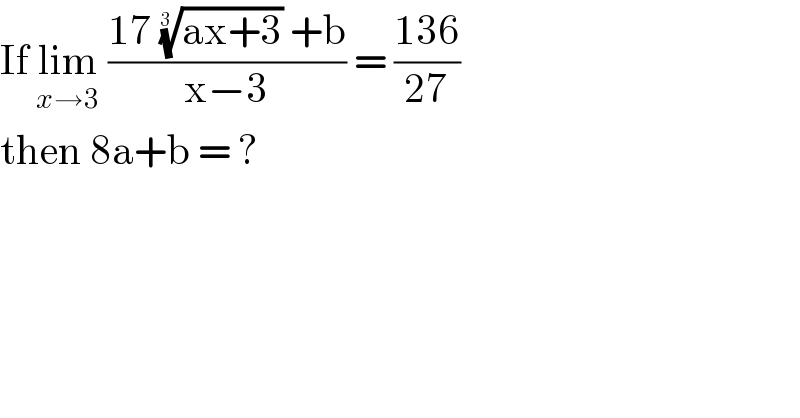
If lim_(x→3) ((17 ((ax+3))^(1/(3 )) +b)/(x−3)) = ((136)/(27)) then 8a+b = ?
$$\mathrm{If}\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{17}\:\sqrt[{\mathrm{3}\:}]{\mathrm{ax}+\mathrm{3}}\:+\mathrm{b}}{\mathrm{x}−\mathrm{3}}\:=\:\frac{\mathrm{136}}{\mathrm{27}} \\ $$$$\mathrm{then}\:\mathrm{8a}+\mathrm{b}\:=\:? \\ $$
Answered by bobhans last updated on 23/Sep/20
limit form (0/0). numerator must be = 0 (1) 17 ((3a+3))^(1/(3 )) +b =0; b ⇒−17 ((3a+3))^(1/(3 )) (2) lim_(x→3) ((17 ((ax+3))^(1/3) −17 ((3a+3))^(1/(3 )) )/(x−3)) =((136)/(27)) lim_(x→3) ((((ax+3))^(1/(3 )) −((3a+3))^(1/(3 )) )/(x−3)) = (8/(27)) set x=3+r ; r→0 lim_(r→0) ((((ar+3a+3))^(1/(3 )) −((3a+3))^(1/(3 )) )/r) = (8/(27)) remember (p)^(1/3) −(q)^(1/(3 )) = ((p−q)/( (p^2 )^(1/(3 )) +((pq))^(1/(3 )) +(q^2 )^(1/(3 )) )) lim_(r→0) (((ar+3a+3)−(3a+3))/(r ((((ar+3a+3)^2 ))^(1/(3 )) +(((3a+3)(ar+3a+3)))^(1/(3 )) +(((3a+3)^2 ))^(1/(3 )) )) =(8/(27)) lim_(r→0) ((ar)/(r((((ar+3a+3)^2 ))^(1/(3 )) +(((ar+3a+3)(3a+3)))^(1/(3 )) +(((3a+3)^2 ))^(1/(3 )) )))=(8/(27)) ⇔ (a/(3 (((3a+3)^2 ))^(1/(3 )) )) = (8/(27)) ; by inspection we get a = 8 , check (8/(3 (((24+3))^(1/(3 )) )^2 )) = (8/(3×9)) = (8/(27)). Then b = −17 ((24+3))^(1/3) =−51 ∴ 8a+b = 64−51=13
$${limit}\:{form}\:\frac{\mathrm{0}}{\mathrm{0}}.\:{numerator}\:{must}\:{be}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{17}\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}{a}+\mathrm{3}}\:+{b}\:=\mathrm{0};\:\:{b}\:\Rightarrow−\mathrm{17}\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}{a}+\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{17}\:\sqrt[{\mathrm{3}}]{{ax}+\mathrm{3}}\:−\mathrm{17}\:\sqrt[{\mathrm{3}\:}]{\mathrm{3}{a}+\mathrm{3}}}{{x}−\mathrm{3}}\:=\frac{\mathrm{136}}{\mathrm{27}} \\ $$$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{{ax}+\mathrm{3}}\:−\sqrt[{\mathrm{3}\:}]{\mathrm{3}{a}+\mathrm{3}}}{{x}−\mathrm{3}}\:=\:\frac{\mathrm{8}}{\mathrm{27}} \\ $$$${set}\:{x}=\mathrm{3}+{r}\:;\:{r}\rightarrow\mathrm{0} \\ $$$$\:\:\:\:\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}\:}]{{ar}+\mathrm{3}{a}+\mathrm{3}}\:−\sqrt[{\mathrm{3}\:}]{\mathrm{3}{a}+\mathrm{3}}}{{r}}\:=\:\frac{\mathrm{8}}{\mathrm{27}} \\ $$$${remember}\:\sqrt[{\mathrm{3}}]{{p}}\:−\sqrt[{\mathrm{3}\:}]{{q}}\:=\:\frac{{p}−{q}}{\:\sqrt[{\mathrm{3}\:}]{{p}^{\mathrm{2}} }+\sqrt[{\mathrm{3}\:}]{{pq}}\:+\sqrt[{\mathrm{3}\:}]{{q}^{\mathrm{2}} }} \\ $$$$\:\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left({ar}+\mathrm{3}{a}+\mathrm{3}\right)−\left(\mathrm{3}{a}+\mathrm{3}\right)}{{r}\:\left(\sqrt[{\mathrm{3}\:}]{\left({ar}+\mathrm{3}{a}+\mathrm{3}\right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}\:}]{\left(\mathrm{3}{a}+\mathrm{3}\right)\left({ar}+\mathrm{3}{a}+\mathrm{3}\right)}+\sqrt[{\mathrm{3}\:}]{\left(\mathrm{3}{a}+\mathrm{3}\right)^{\mathrm{2}} }\right.}\:=\frac{\mathrm{8}}{\mathrm{27}} \\ $$$$\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{ar}}{{r}\left(\sqrt[{\mathrm{3}\:}]{\left({ar}+\mathrm{3}{a}+\mathrm{3}\right)^{\mathrm{2}} }+\sqrt[{\mathrm{3}\:}]{\left({ar}+\mathrm{3}{a}+\mathrm{3}\right)\left(\mathrm{3}{a}+\mathrm{3}\right)}+\sqrt[{\mathrm{3}\:}]{\left(\mathrm{3}{a}+\mathrm{3}\right)^{\mathrm{2}} }\right)}=\frac{\mathrm{8}}{\mathrm{27}} \\ $$$$\Leftrightarrow\:\frac{{a}}{\mathrm{3}\:\sqrt[{\mathrm{3}\:}]{\left(\mathrm{3}{a}+\mathrm{3}\right)^{\mathrm{2}} }}\:=\:\frac{\mathrm{8}}{\mathrm{27}}\:; \\ $$$${by}\:{inspection}\:{we}\:{get}\:{a}\:=\:\mathrm{8}\:,\:{check}\:\frac{\mathrm{8}}{\mathrm{3}\:\left(\sqrt[{\mathrm{3}\:}]{\mathrm{24}+\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{8}}{\mathrm{3}×\mathrm{9}}\:=\:\frac{\mathrm{8}}{\mathrm{27}}.\:{Then}\:{b}\:=\:−\mathrm{17}\:\sqrt[{\mathrm{3}}]{\mathrm{24}+\mathrm{3}}\:=−\mathrm{51} \\ $$$$\therefore\:\mathrm{8}{a}+{b}\:=\:\mathrm{64}−\mathrm{51}=\mathrm{13} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *