Question Number 99341 by bemath last updated on 20/Jun/20
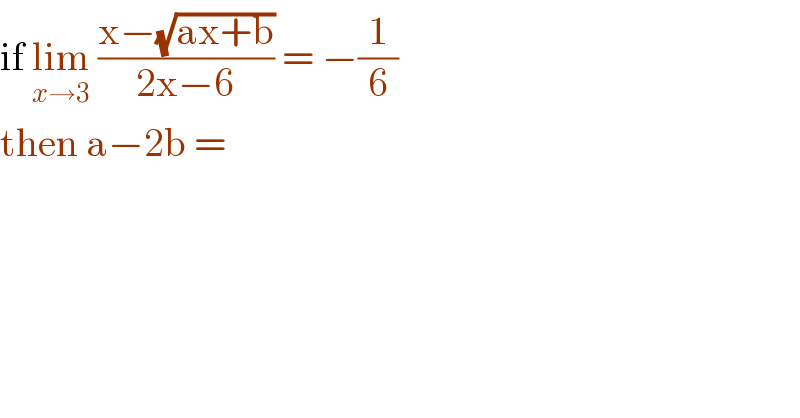
$$\mathrm{if}\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{x}−\sqrt{\mathrm{ax}+\mathrm{b}}}{\mathrm{2x}−\mathrm{6}}\:=\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\mathrm{then}\:\mathrm{a}−\mathrm{2b}\:=\: \\ $$
Commented by bobhans last updated on 20/Jun/20
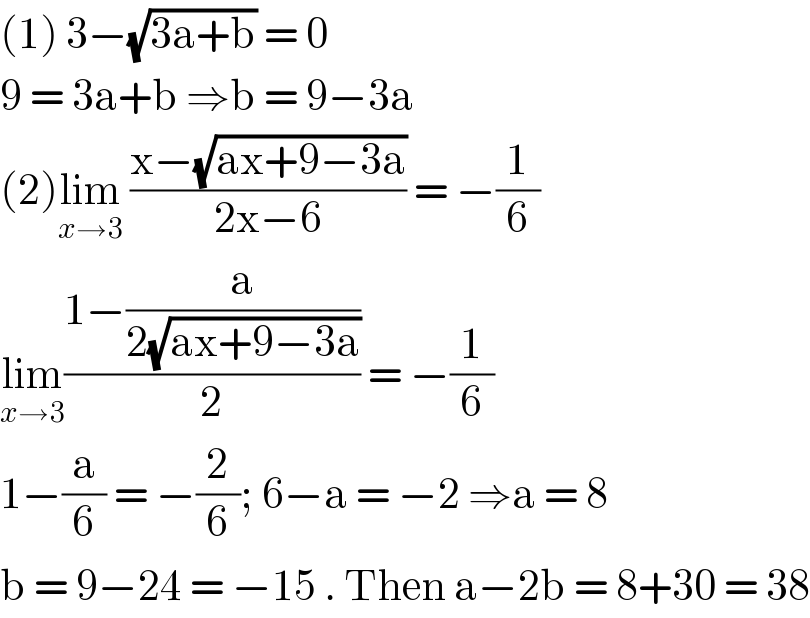
$$\left(\mathrm{1}\right)\:\mathrm{3}−\sqrt{\mathrm{3a}+\mathrm{b}}\:=\:\mathrm{0}\: \\ $$$$\mathrm{9}\:=\:\mathrm{3a}+\mathrm{b}\:\Rightarrow\mathrm{b}\:=\:\mathrm{9}−\mathrm{3a} \\ $$$$\left(\mathrm{2}\right)\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\mathrm{x}−\sqrt{\mathrm{ax}+\mathrm{9}−\mathrm{3a}}}{\mathrm{2x}−\mathrm{6}}\:=\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{a}}{\mathrm{2}\sqrt{\mathrm{ax}+\mathrm{9}−\mathrm{3a}}}}{\mathrm{2}}\:=\:−\frac{\mathrm{1}}{\mathrm{6}}\: \\ $$$$\mathrm{1}−\frac{\mathrm{a}}{\mathrm{6}}\:=\:−\frac{\mathrm{2}}{\mathrm{6}};\:\mathrm{6}−\mathrm{a}\:=\:−\mathrm{2}\:\Rightarrow\mathrm{a}\:=\:\mathrm{8}\: \\ $$$$\mathrm{b}\:=\:\mathrm{9}−\mathrm{24}\:=\:−\mathrm{15}\:.\:\mathrm{Then}\:\mathrm{a}−\mathrm{2b}\:=\:\mathrm{8}+\mathrm{30}\:=\:\mathrm{38} \\ $$
