Question Number 125575 by ZiYangLee last updated on 12/Dec/20
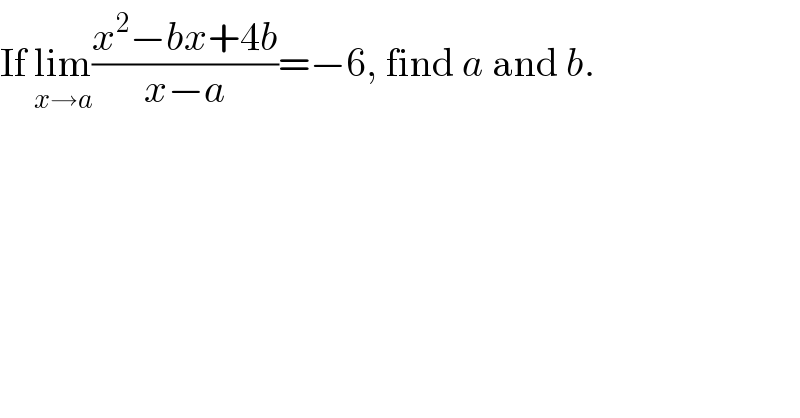
$$\mathrm{If}\:\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} −{bx}+\mathrm{4}{b}}{{x}−{a}}=−\mathrm{6},\:\mathrm{find}\:{a}\:\mathrm{and}\:{b}. \\ $$
Answered by ajfour last updated on 12/Dec/20
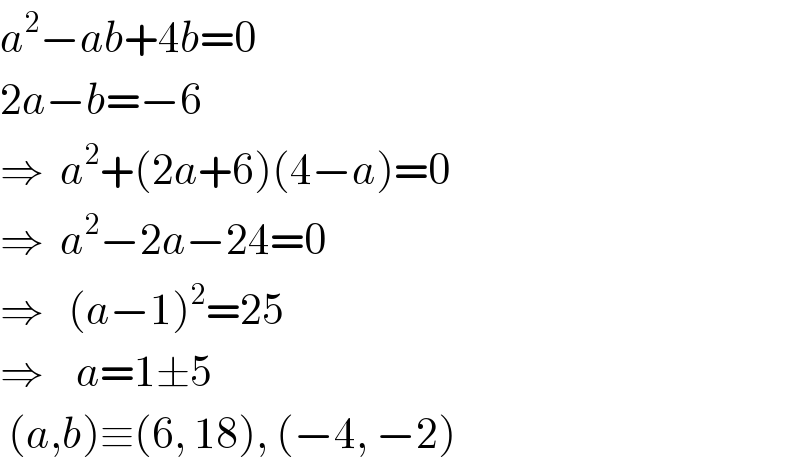
$${a}^{\mathrm{2}} −{ab}+\mathrm{4}{b}=\mathrm{0} \\ $$$$\mathrm{2}{a}−{b}=−\mathrm{6} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} +\left(\mathrm{2}{a}+\mathrm{6}\right)\left(\mathrm{4}−{a}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{a}^{\mathrm{2}} −\mathrm{2}{a}−\mathrm{24}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\left({a}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\Rightarrow\:\:\:\:{a}=\mathrm{1}\pm\mathrm{5} \\ $$$$\:\left({a},{b}\right)\equiv\left(\mathrm{6},\:\mathrm{18}\right),\:\left(−\mathrm{4},\:−\mathrm{2}\right) \\ $$
