If-M-and-m-are-respectively-the-largest-and-the-smallest-integers-that-satisfying-the-inequality-6n-2-5n-99-find-the-value-of-M-m-

Question Number 119835 by ZiYangLee last updated on 27/Oct/20

$$\mathrm{If}\:{M}\:\mathrm{and}\:{m}\:\mathrm{are}\:\mathrm{respectively}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{smallest}\:\mathrm{integers}\:\mathrm{that}\:\mathrm{satisfying}\:\mathrm{the} \\ $$$$\mathrm{inequality}\:\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}\leqslant\mathrm{99},\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$${M}−{m}. \\ $$

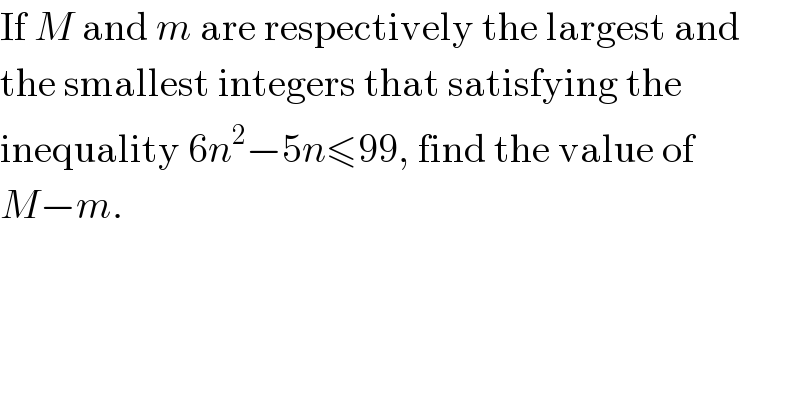
Commented by talminator2856791 last updated on 27/Oct/20

$$\mathrm{is}\:\mathrm{the}\:\mathrm{question}\:\mathrm{correctly}\:\mathrm{stated}? \\ $$

Answered by TANMAY PANACEA last updated on 27/Oct/20

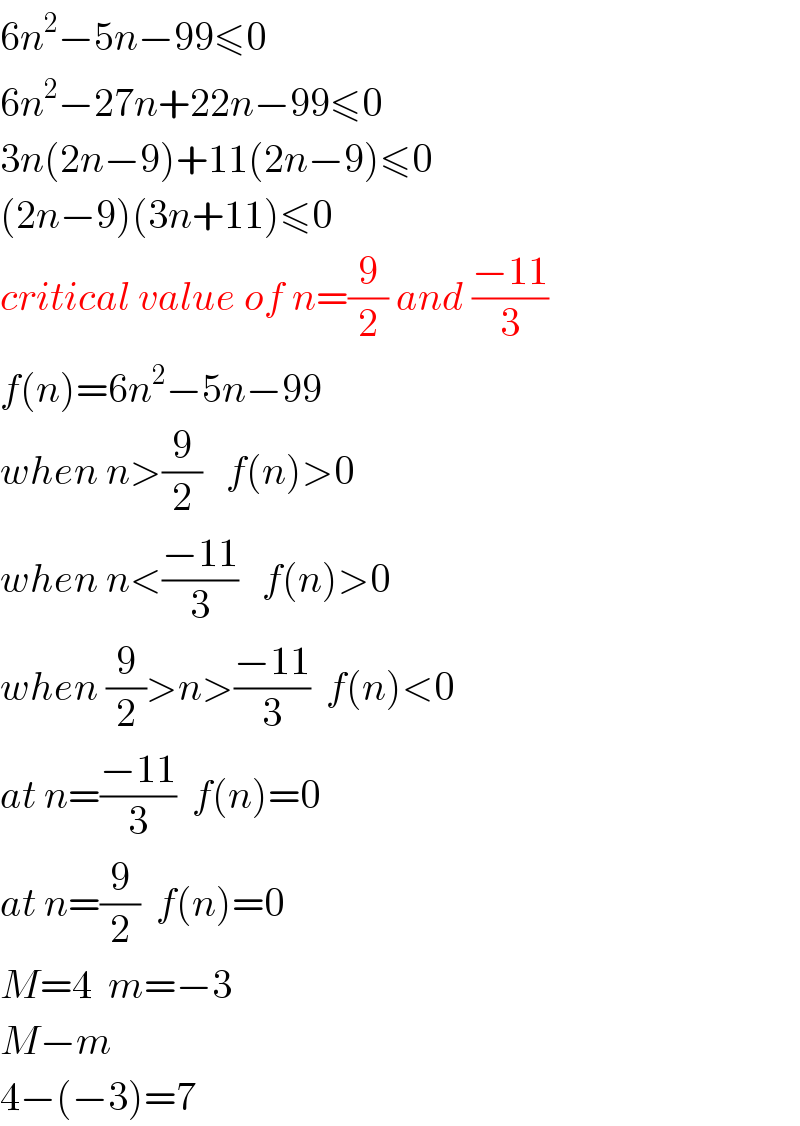
6n^2 −5n−99≤0 6n^2 −27n+22n−99≤0 3n(2n−9)+11(2n−9)≤0 (2n−9)(3n+11)≤0 critical value of n=(9/2) and ((−11)/3) f(n)=6n^2 −5n−99 when n>(9/2) f(n)>0 when n<((−11)/3) f(n)>0 when (9/2)>n>((−11)/3) f(n)<0 at n=((−11)/3) f(n)=0 at n=(9/2) f(n)=0 M=4 m=−3 M−m 4−(−3)=7

$$\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}−\mathrm{99}\leqslant\mathrm{0} \\ $$$$\mathrm{6}{n}^{\mathrm{2}} −\mathrm{27}{n}+\mathrm{22}{n}−\mathrm{99}\leqslant\mathrm{0} \\ $$$$\mathrm{3}{n}\left(\mathrm{2}{n}−\mathrm{9}\right)+\mathrm{11}\left(\mathrm{2}{n}−\mathrm{9}\right)\leqslant\mathrm{0} \\ $$$$\left(\mathrm{2}{n}−\mathrm{9}\right)\left(\mathrm{3}{n}+\mathrm{11}\right)\leqslant\mathrm{0} \\ $$$${critical}\:{value}\:{of}\:{n}=\frac{\mathrm{9}}{\mathrm{2}}\:{and}\:\frac{−\mathrm{11}}{\mathrm{3}} \\ $$$${f}\left({n}\right)=\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}−\mathrm{99} \\ $$$${when}\:{n}>\frac{\mathrm{9}}{\mathrm{2}}\:\:\:{f}\left({n}\right)>\mathrm{0} \\ $$$${when}\:{n}<\frac{−\mathrm{11}}{\mathrm{3}}\:\:\:{f}\left({n}\right)>\mathrm{0} \\ $$$${when}\:\frac{\mathrm{9}}{\mathrm{2}}>{n}>\frac{−\mathrm{11}}{\mathrm{3}}\:\:{f}\left({n}\right)<\mathrm{0} \\ $$$${at}\:{n}=\frac{−\mathrm{11}}{\mathrm{3}}\:\:{f}\left({n}\right)=\mathrm{0} \\ $$$${at}\:{n}=\frac{\mathrm{9}}{\mathrm{2}}\:\:{f}\left({n}\right)=\mathrm{0} \\ $$$${M}=\mathrm{4}\:\:{m}=−\mathrm{3} \\ $$$${M}−{m} \\ $$$$\mathrm{4}−\left(−\mathrm{3}\right)=\mathrm{7} \\ $$

Commented by ZiYangLee last updated on 27/Oct/20

$$\mathrm{Correct}! \\ $$

Commented by TANMAY PANACEA last updated on 27/Oct/20

$${thank}\:{you}\:{sir} \\ $$

Answered by Olaf last updated on 27/Oct/20

6n^2 −5n−99 = 0 Δ = 25−4×6×(−99) = 2401 = 49^2 n_1 = ((5−49)/(12)) = −((11)/3) n_2 = ((5+49)/(12)) = (9/2) ⇒ 6n^2 −5n ≤ 99 if n∈[−((11)/3);+(9/2)] M = n_(max) = 4 m = n_(min) = −3 (if m∈Z) M−m = 4−(−3) = 7 (or 4 if m∈N)

$$\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}−\mathrm{99}\:=\:\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{25}−\mathrm{4}×\mathrm{6}×\left(−\mathrm{99}\right)\:=\:\mathrm{2401}\:=\:\mathrm{49}^{\mathrm{2}} \\ $$$${n}_{\mathrm{1}} \:=\:\frac{\mathrm{5}−\mathrm{49}}{\mathrm{12}}\:=\:−\frac{\mathrm{11}}{\mathrm{3}} \\ $$$${n}_{\mathrm{2}} \:=\:\frac{\mathrm{5}+\mathrm{49}}{\mathrm{12}}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{6}{n}^{\mathrm{2}} −\mathrm{5}{n}\:\leqslant\:\mathrm{99}\:\mathrm{if}\:{n}\in\left[−\frac{\mathrm{11}}{\mathrm{3}};+\frac{\mathrm{9}}{\mathrm{2}}\right] \\ $$$$\mathrm{M}\:=\:{n}_{{max}} \:=\:\mathrm{4} \\ $$$${m}\:=\:{n}_{{min}} \:=\:−\mathrm{3}\:\left(\mathrm{if}\:{m}\in\mathbb{Z}\right) \\ $$$$\mathrm{M}−{m}\:=\:\mathrm{4}−\left(−\mathrm{3}\right)\:=\:\mathrm{7} \\ $$$$\left(\mathrm{or}\:\mathrm{4}\:\mathrm{if}\:{m}\in\mathbb{N}\right) \\ $$

Facebook Tweet Pin

If-M-and-m-are-respectively-the-largest-and-the-smallest-integers-that-satisfying-the-inequality-6n-2-5n-99-find-the-value-of-M-m-

Leave a Reply Cancel reply