Question Number 79625 by M±th+et£s last updated on 26/Jan/20
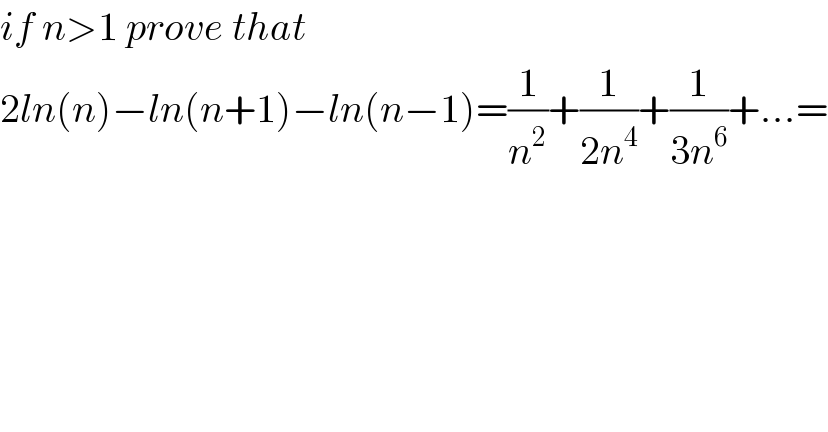
$${if}\:{n}>\mathrm{1}\:{prove}\:{that} \\ $$$$\mathrm{2}{ln}\left({n}\right)−{ln}\left({n}+\mathrm{1}\right)−{ln}\left({n}−\mathrm{1}\right)=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{6}} }+…= \\ $$
Answered by mind is power last updated on 27/Jan/20
![⇔ln((n^2 /(n^2 −1)))=ln((1/(1−(1/n^2 ))))=−ln(1−(1/n^2 )) ∀n∈N−{0,1} (1/n)<1⇒(1/n^2 )<1 −ln(1−x)=Σ_(k≥1) (x^k /k),∀x∈]−1,1[,x=(1/n^2 )⇒ −ln(1−(1/n^2 ))=Σ_(k≥1) (1/(n^(2k) .k))=(1/n^2 )+(1/(2n^4 ))+..........](https://www.tinkutara.com/question/Q79655.png)
$$\Leftrightarrow{ln}\left(\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} −\mathrm{1}}\right)={ln}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}\right)=−{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right) \\ $$$$\forall{n}\in\mathbb{N}−\left\{\mathrm{0},\mathrm{1}\right\}\:\:\:\frac{\mathrm{1}}{{n}}<\mathrm{1}\Rightarrow\frac{\mathrm{1}}{{n}^{\mathrm{2}} }<\mathrm{1} \\ $$$$\left.−{ln}\left(\mathrm{1}−{x}\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{k}} }{{k}},\forall{x}\in\right]−\mathrm{1},\mathrm{1}\left[,{x}=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\Rightarrow\right. \\ $$$$−{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}{k}} .{k}}=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }+………. \\ $$$$ \\ $$
