Question Number 93315 by Shakhzod last updated on 12/May/20
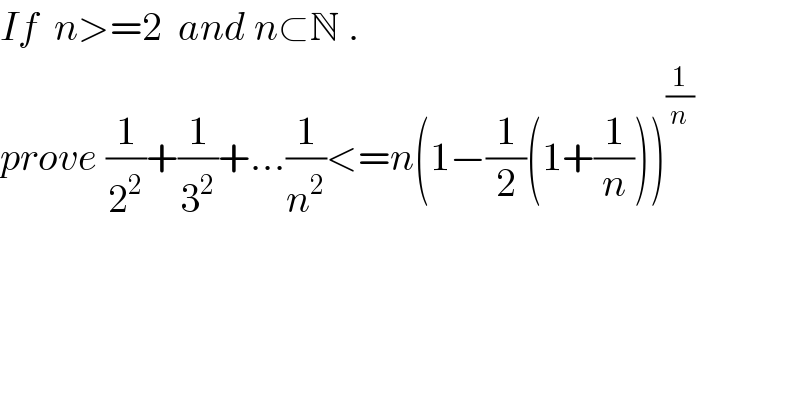
$${If}\:\:{n}>=\mathrm{2}\:\:{and}\:{n}\subset\mathbb{N}\:. \\ $$$${prove}\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…\frac{\mathrm{1}}{{n}^{\mathrm{2}} }<={n}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\right)^{\frac{\mathrm{1}}{{n}}} \\ $$
