Menu Close

If-n-Z-show-that-k-1-n-ln-2-1-1-k-lt-1-

Tinku Tara 0 Comments
Pin




Question Number 107481 by ZiYangLee last updated on 11/Aug/20
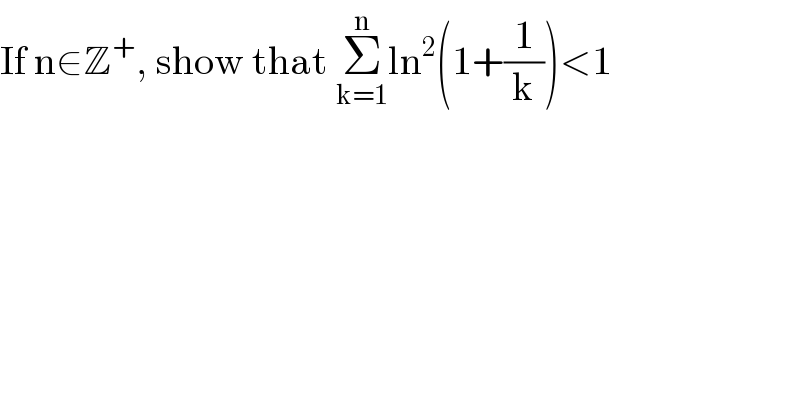
If n∈Z^+ , show that Σ_(k=1) ^n ln^2 (1+(1/k))<1
$$\mathrm{If}\:\mathrm{n}\in\mathbb{Z}^{+} ,\:\mathrm{show}\:\mathrm{that}\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)<\mathrm{1} \\ $$
Answered by 1549442205PVT last updated on 11/Aug/20
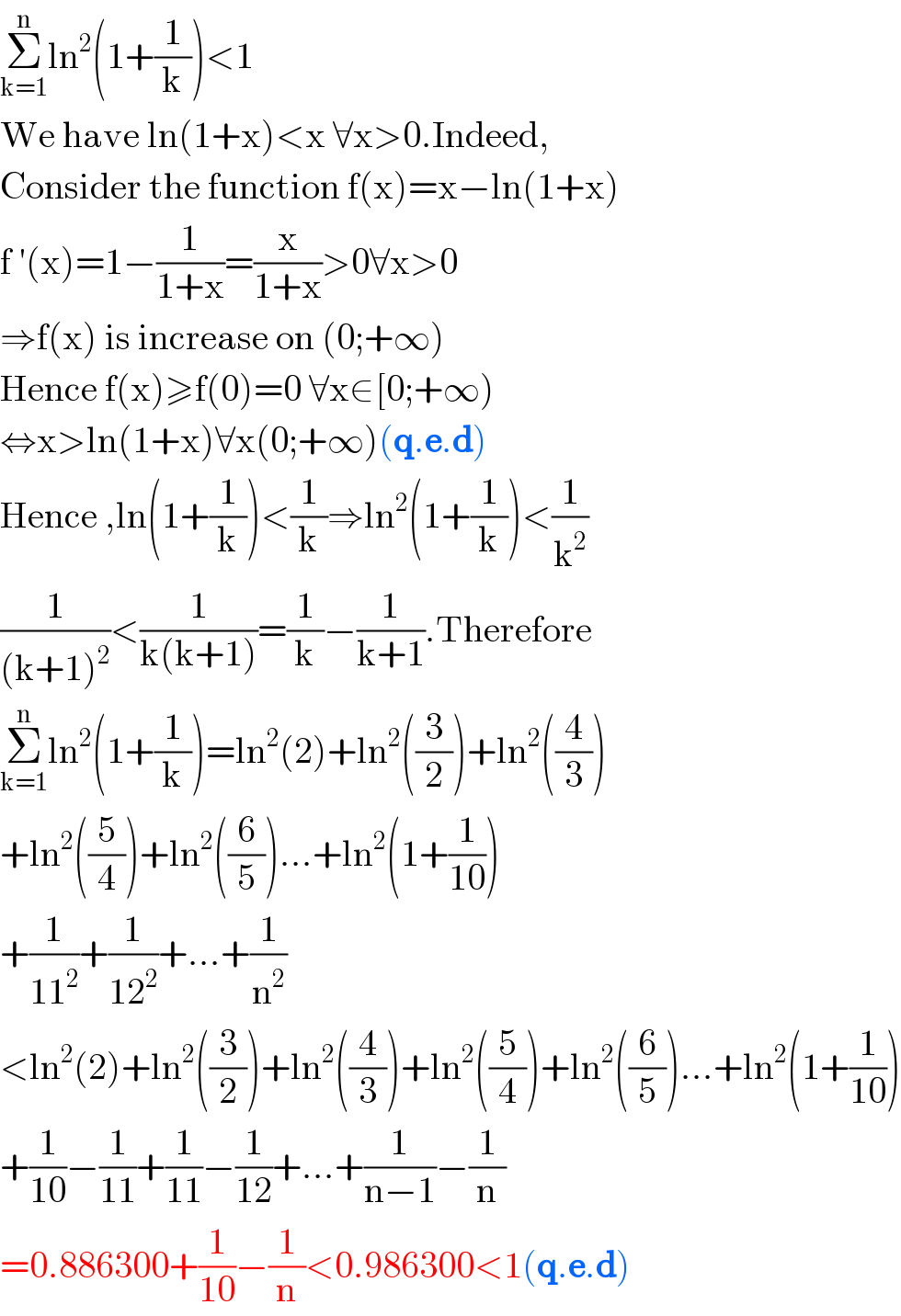
Σ_(k=1) ^n ln^2 (1+(1/k))<1 We have ln(1+x)<x ∀x>0.Indeed, Consider the function f(x)=x−ln(1+x) f ′(x)=1−(1/(1+x))=(x/(1+x))>0∀x>0 ⇒f(x) is increase on (0;+∞) Hence f(x)≥f(0)=0 ∀x∈[0;+∞) ⇔x>ln(1+x)∀x(0;+∞)(q.e.d) Hence ,ln(1+(1/k))<(1/k)⇒ln^2 (1+(1/k))<(1/k^2 ) (1/((k+1)^2 ))<(1/(k(k+1)))=(1/k)−(1/(k+1)).Therefore Σ_(k=1) ^n ln^2 (1+(1/k))=ln^2 (2)+ln^2 ((3/2))+ln^2 ((4/3)) +ln^2 ((5/4))+ln^2 ((6/5))...+ln^2 (1+(1/(10))) +(1/(11^2 ))+(1/(12^2 ))+...+(1/n^2 ) <ln^2 (2)+ln^2 ((3/2))+ln^2 ((4/3))+ln^2 ((5/4))+ln^2 ((6/5))...+ln^2 (1+(1/(10))) +(1/(10))−(1/(11))+(1/(11))−(1/(12))+...+(1/(n−1))−(1/n) =0.886300+(1/(10))−(1/n)<0.986300<1(q.e.d)
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)<\mathrm{1} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)<\mathrm{x}\:\forall\mathrm{x}>\mathrm{0}.\mathrm{Indeed}, \\ $$$$\mathrm{Consider}\:\mathrm{the}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right) \\ $$$$\mathrm{f}\:'\left(\mathrm{x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}}>\mathrm{0}\forall\mathrm{x}>\mathrm{0} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{increase}\:\mathrm{on}\:\left(\mathrm{0};+\infty\right) \\ $$$$\mathrm{Hence}\:\mathrm{f}\left(\mathrm{x}\right)\geqslant\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0}\:\forall\mathrm{x}\in\left[\mathrm{0};+\infty\right) \\ $$$$\Leftrightarrow\mathrm{x}>\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\forall\mathrm{x}\left(\mathrm{0};+\infty\right)\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$$$\mathrm{Hence}\:,\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)<\frac{\mathrm{1}}{\mathrm{k}}\Rightarrow\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)<\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }<\frac{\mathrm{1}}{\mathrm{k}\left(\mathrm{k}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}.\mathrm{Therefore} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{k}}\right)=\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$$$+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{5}}{\mathrm{4}}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{6}}{\mathrm{5}}\right)…+\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{12}^{\mathrm{2}} }+…+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$<\mathrm{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{5}}{\mathrm{4}}\right)+\mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{6}}{\mathrm{5}}\right)…+\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{11}}+\frac{\mathrm{1}}{\mathrm{11}}−\frac{\mathrm{1}}{\mathrm{12}}+…+\frac{\mathrm{1}}{\mathrm{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$=\mathrm{0}.\mathrm{886300}+\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{n}}<\mathrm{0}.\mathrm{986300}<\mathrm{1}\left(\boldsymbol{\mathrm{q}}.\boldsymbol{\mathrm{e}}.\boldsymbol{\mathrm{d}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *