If-outer-angle-in-n-polygone-is-18-find-n-

Question Number 175893 by blackmamba last updated on 08/Sep/22

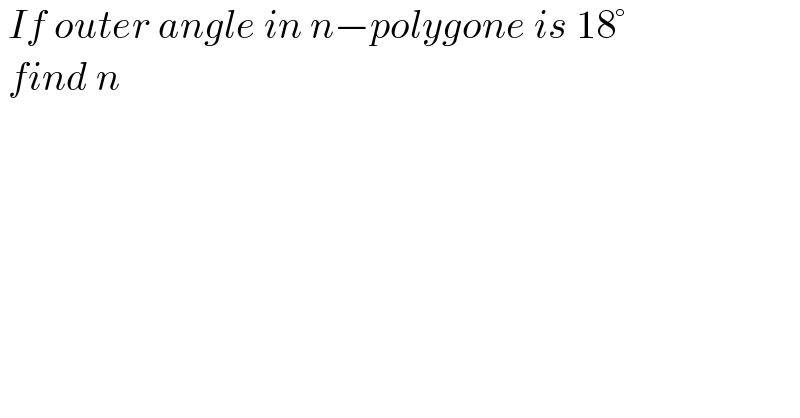
I f o u t e r a n g l e i n n - p o l y g o n e i s 18 °

f i n d n

Commented by Rasheed.Sindhi last updated on 09/Sep/22

n = 20

Commented by blackmamba last updated on 09/Sep/22

w h a t t h e f o r m u l a

Commented by BaliramKumar last updated on 09/Sep/22

\frac{360}{18} = 20

Answered by Rasheed.Sindhi last updated on 09/Sep/22

C e n t r a l a n g l e : 360 / n

A n g l e b e t w e e n c o n s e c u t i v e s i d e s :

180 - \frac{360}{n} = \frac{180 n - 360}{n}

o u t e r a n g l e : 180 - \frac{180 n - 360}{n}

= \frac{180 n - 180 n + 360}{n} = \frac{360}{n}

\frac{360}{n} = 18 \Rightarrow n = \frac{360}{18} = 20

\begin{matrix} \underset{\overset{}{n = \frac{360}{Outer angle}}}{Outer angle = \frac{360}{n}} \end{matrix}

Commented by peter frank last updated on 09/Sep/22

thanks

Commented by Tawa11 last updated on 15/Sep/22

Great sir .

Facebook Tweet Pin