Menu Close

if-p-5i-j-3k-and-q-i-3j-5k-then-find-the-value-of-so-that-p-q-and-p-q-are-perpendicular-vectors-

Tinku Tara 0 Comments
Pin




Question Number 118161 by gopikrishnan last updated on 15/Oct/20
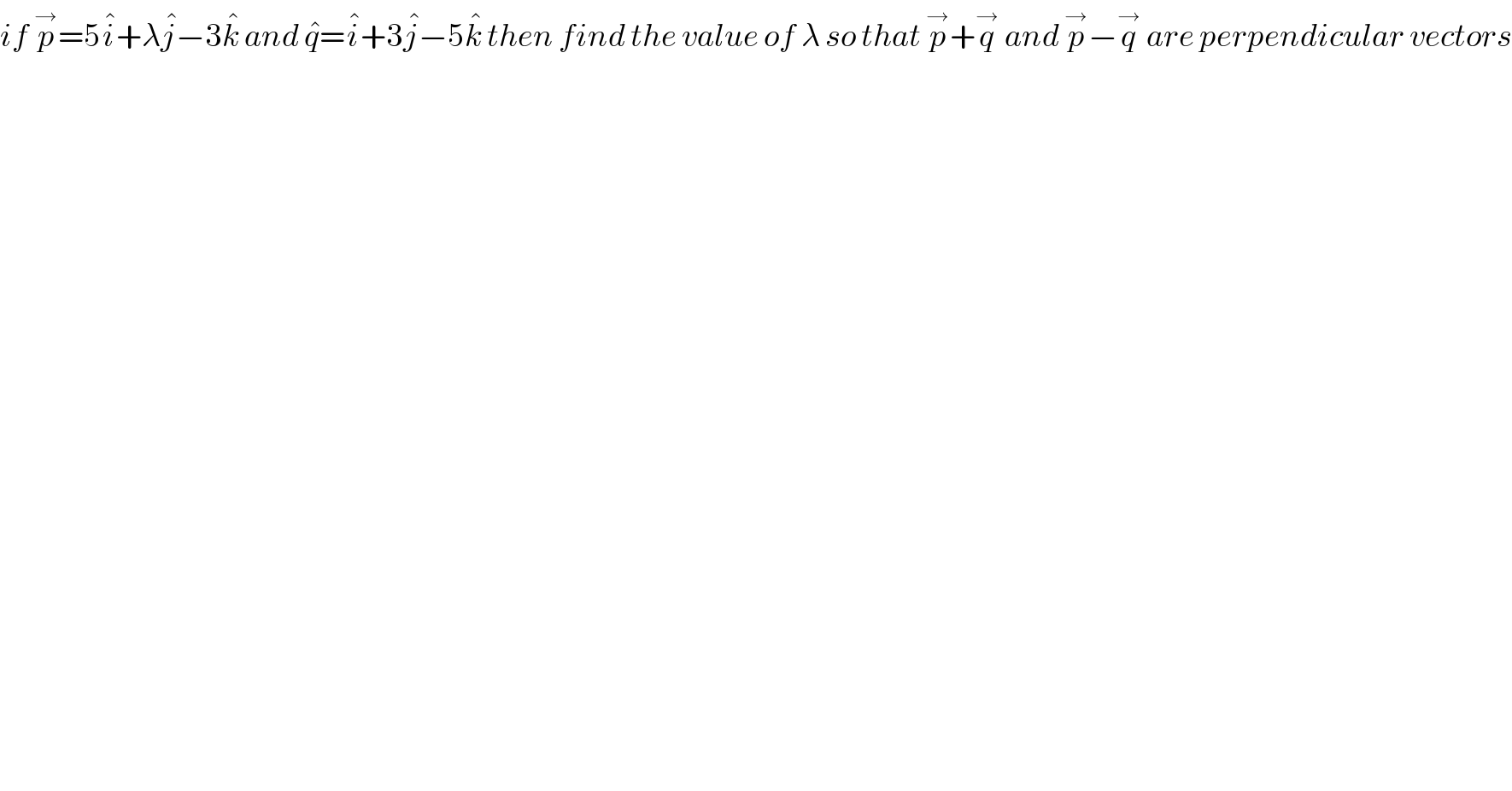
if p^→ =5i^� +λj^� −3k^� and q^� =i^� +3j^� −5k^� then find the value of λ so that p^→ +q^→ and p^→ −q^→ are perpendicular vectors
$${if}\:\overset{\rightarrow} {{p}}=\mathrm{5}\hat {{i}}+\lambda\hat {{j}}−\mathrm{3}\hat {{k}}\:{and}\:\hat {{q}}=\hat {{i}}+\mathrm{3}\hat {{j}}−\mathrm{5}\hat {{k}}\:{then}\:{find}\:{the}\:{value}\:{of}\:\lambda\:{so}\:{that}\:\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}\:{and}\:\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\:{are}\:{perpendicular}\:{vectors} \\ $$
Answered by Dwaipayan Shikari last updated on 15/Oct/20
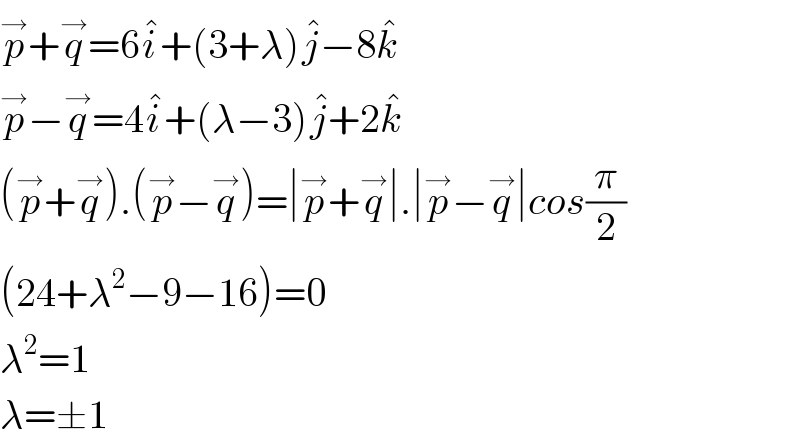
p^→ +q^→ =6i^� +(3+λ)j^� −8k^� p^→ −q^→ =4i^� +(λ−3)j^� +2k^� (p^→ +q^→ ).(p^→ −q^→ )=∣p^→ +q^→ ∣.∣p^→ −q^→ ∣cos(π/2) (24+λ^2 −9−16)=0 λ^2 =1 λ=±1
$$\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}=\mathrm{6}\hat {{i}}+\left(\mathrm{3}+\lambda\right)\hat {{j}}−\mathrm{8}\hat {{k}} \\ $$$$\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}=\mathrm{4}\hat {{i}}+\left(\lambda−\mathrm{3}\right)\hat {{j}}+\mathrm{2}\hat {{k}} \\ $$$$\left(\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}\right).\left(\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\right)=\mid\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}\mid.\mid\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\mid{cos}\frac{\pi}{\mathrm{2}} \\ $$$$\left(\mathrm{24}+\lambda^{\mathrm{2}} −\mathrm{9}−\mathrm{16}\right)=\mathrm{0} \\ $$$$\lambda^{\mathrm{2}} =\mathrm{1} \\ $$$$\lambda=\pm\mathrm{1} \\ $$
Answered by Rio Michael last updated on 15/Oct/20
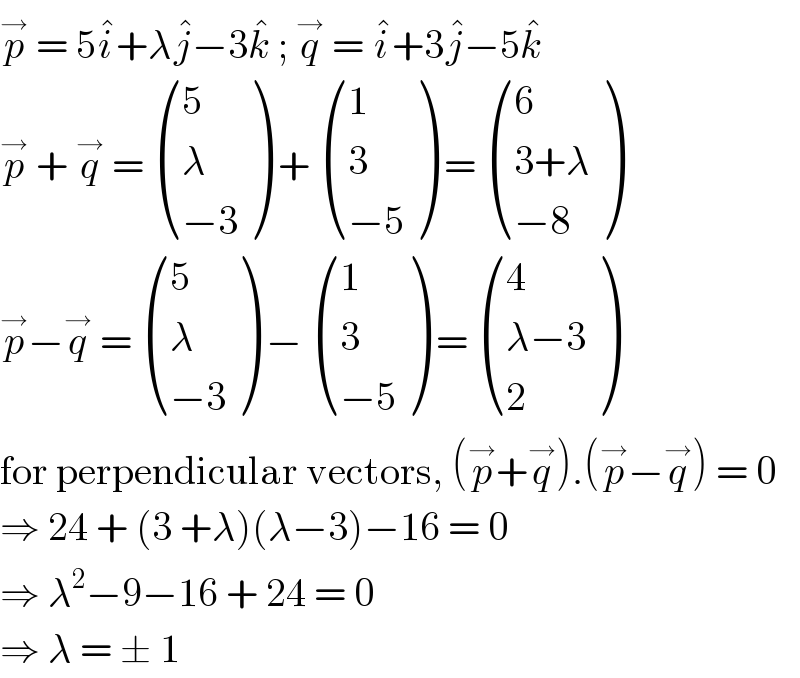
p^→ = 5i^� +λj^� −3k^� ; q^→ = i^� +3j^� −5k^� p^→ + q^→ = ((5),(λ),((−3)) ) + ((1),(3),((−5)) ) = ((6),((3+λ)),((−8)) ) p^→ −q^→ = ((5),(λ),((−3)) ) − ((1),(3),((−5)) ) = ((4),((λ−3)),(2) ) for perpendicular vectors, (p^→ +q^→ ).(p^→ −q^→ ) = 0 ⇒ 24 + (3 +λ)(λ−3)−16 = 0 ⇒ λ^2 −9−16 + 24 = 0 ⇒ λ = ± 1
$$\overset{\rightarrow} {{p}}\:=\:\mathrm{5}\hat {{i}}+\lambda\hat {{j}}−\mathrm{3}\hat {{k}}\:;\:\overset{\rightarrow} {{q}}\:=\:\hat {{i}}+\mathrm{3}\hat {{j}}−\mathrm{5}\hat {{k}} \\ $$$$\overset{\rightarrow} {{p}}\:+\:\overset{\rightarrow} {{q}}\:=\:\begin{pmatrix}{\mathrm{5}}\\{\lambda}\\{−\mathrm{3}}\end{pmatrix}\:+\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{3}}\\{−\mathrm{5}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{6}}\\{\mathrm{3}+\lambda}\\{−\mathrm{8}}\end{pmatrix} \\ $$$$\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\:=\:\begin{pmatrix}{\mathrm{5}}\\{\lambda}\\{−\mathrm{3}}\end{pmatrix}\:−\:\begin{pmatrix}{\mathrm{1}}\\{\mathrm{3}}\\{−\mathrm{5}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{4}}\\{\lambda−\mathrm{3}}\\{\mathrm{2}}\end{pmatrix} \\ $$$$\mathrm{for}\:\mathrm{perpendicular}\:\mathrm{vectors},\:\left(\overset{\rightarrow} {{p}}+\overset{\rightarrow} {{q}}\right).\left(\overset{\rightarrow} {{p}}−\overset{\rightarrow} {{q}}\right)\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{24}\:+\:\left(\mathrm{3}\:+\lambda\right)\left(\lambda−\mathrm{3}\right)−\mathrm{16}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\lambda^{\mathrm{2}} −\mathrm{9}−\mathrm{16}\:+\:\mathrm{24}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\lambda\:=\:\pm\:\mathrm{1}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *