Menu Close

If-p-cos-i-sin-and-q-cos-i-sin-Show-that-i-p-q-p-q-i-tan-2-ii-p-q-pq-1-p-q-pq-1-sin-sin-sin

Tinku Tara 0 Comments
Pin




Question Number 51905 by Tawa1 last updated on 01/Jan/19
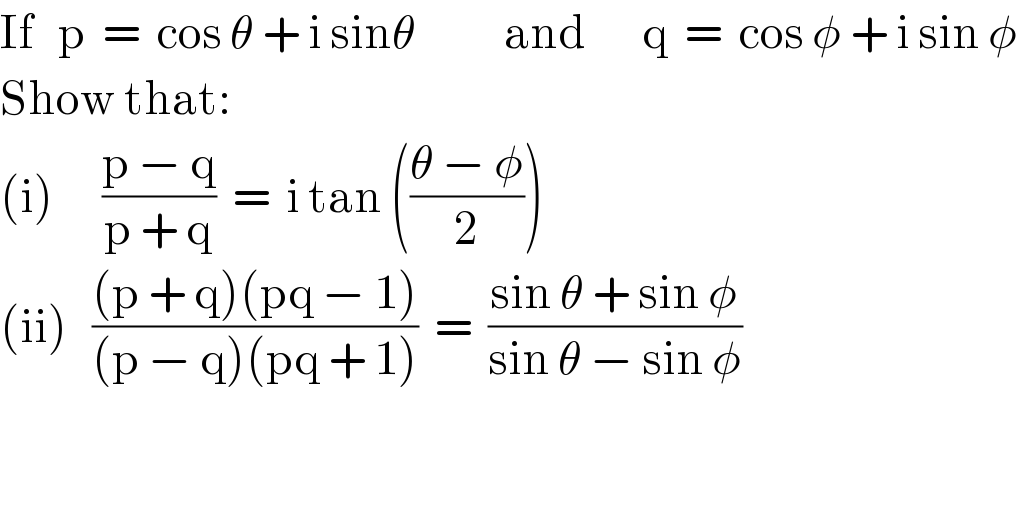
If p = cos θ + i sinθ and q = cos φ + i sin φ Show that: (i) ((p − q)/(p + q)) = i tan (((θ − φ)/2)) (ii) (((p + q)(pq − 1))/((p − q)(pq + 1))) = ((sin θ + sin φ)/(sin θ − sin φ))
$$\mathrm{If}\:\:\:\mathrm{p}\:\:=\:\:\mathrm{cos}\:\theta\:+\:\mathrm{i}\:\mathrm{sin}\theta\:\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:\:\:\:\:\:\:\mathrm{q}\:\:=\:\:\mathrm{cos}\:\phi\:+\:\mathrm{i}\:\mathrm{sin}\:\phi \\ $$$$\mathrm{Show}\:\mathrm{that}: \\ $$$$\left(\mathrm{i}\right)\:\:\:\:\:\:\frac{\mathrm{p}\:−\:\mathrm{q}}{\mathrm{p}\:+\:\mathrm{q}}\:\:=\:\:\mathrm{i}\:\mathrm{tan}\:\left(\frac{\theta\:−\:\phi}{\mathrm{2}}\right) \\ $$$$\left(\mathrm{ii}\right)\:\:\:\frac{\left(\mathrm{p}\:+\:\mathrm{q}\right)\left(\mathrm{pq}\:−\:\mathrm{1}\right)}{\left(\mathrm{p}\:−\:\mathrm{q}\right)\left(\mathrm{pq}\:+\:\mathrm{1}\right)}\:\:=\:\:\frac{\mathrm{sin}\:\theta\:+\:\mathrm{sin}\:\phi}{\mathrm{sin}\:\theta\:−\:\mathrm{sin}\:\phi} \\ $$
Answered by Kunal12588 last updated on 01/Jan/19
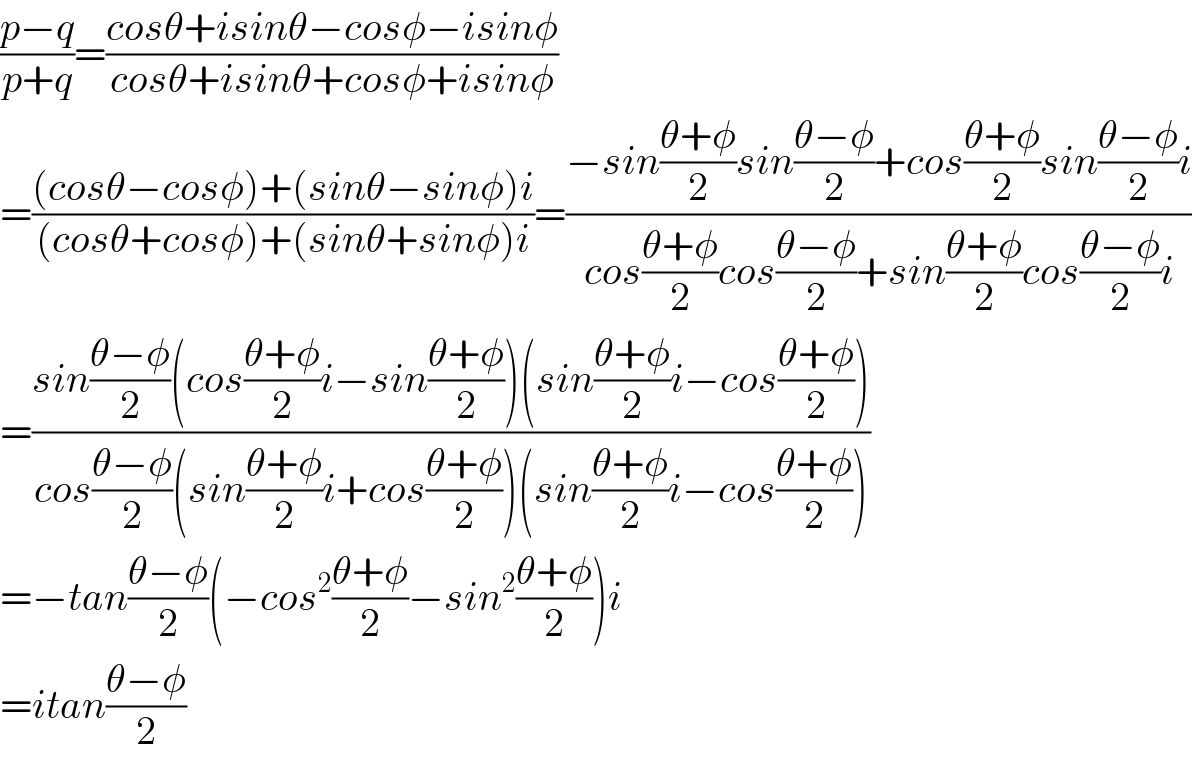
((p−q)/(p+q))=((cosθ+isinθ−cosφ−isinφ)/(cosθ+isinθ+cosφ+isinφ)) =(((cosθ−cosφ)+(sinθ−sinφ)i)/((cosθ+cosφ)+(sinθ+sinφ)i))=((−sin((θ+φ)/2)sin((θ−φ)/2)+cos((θ+φ)/2)sin((θ−φ)/2)i)/(cos((θ+φ)/2)cos((θ−φ)/2)+sin((θ+φ)/2)cos((θ−φ)/2)i)) =((sin((θ−φ)/2)(cos((θ+φ)/2)i−sin((θ+φ)/2))(sin((θ+φ)/2)i−cos((θ+φ)/2)))/(cos((θ−φ)/2)(sin((θ+φ)/2)i+cos((θ+φ)/2))(sin((θ+φ)/2)i−cos((θ+φ)/2)))) =−tan((θ−φ)/2)(−cos^2 ((θ+φ)/2)−sin^2 ((θ+φ)/2))i =itan((θ−φ)/2)
$$\frac{{p}−{q}}{{p}+{q}}=\frac{{cos}\theta+{isin}\theta−{cos}\phi−{isin}\phi}{{cos}\theta+{isin}\theta+{cos}\phi+{isin}\phi} \\ $$$$=\frac{\left({cos}\theta−{cos}\phi\right)+\left({sin}\theta−{sin}\phi\right){i}}{\left({cos}\theta+{cos}\phi\right)+\left({sin}\theta+{sin}\phi\right){i}}=\frac{−{sin}\frac{\theta+\phi}{\mathrm{2}}{sin}\frac{\theta−\phi}{\mathrm{2}}+{cos}\frac{\theta+\phi}{\mathrm{2}}{sin}\frac{\theta−\phi}{\mathrm{2}}{i}}{{cos}\frac{\theta+\phi}{\mathrm{2}}{cos}\frac{\theta−\phi}{\mathrm{2}}+{sin}\frac{\theta+\phi}{\mathrm{2}}{cos}\frac{\theta−\phi}{\mathrm{2}}{i}} \\ $$$$=\frac{{sin}\frac{\theta−\phi}{\mathrm{2}}\left({cos}\frac{\theta+\phi}{\mathrm{2}}{i}−{sin}\frac{\theta+\phi}{\mathrm{2}}\right)\left({sin}\frac{\theta+\phi}{\mathrm{2}}{i}−{cos}\frac{\theta+\phi}{\mathrm{2}}\right)}{{cos}\frac{\theta−\phi}{\mathrm{2}}\left({sin}\frac{\theta+\phi}{\mathrm{2}}{i}+{cos}\frac{\theta+\phi}{\mathrm{2}}\right)\left({sin}\frac{\theta+\phi}{\mathrm{2}}{i}−{cos}\frac{\theta+\phi}{\mathrm{2}}\right)} \\ $$$$=−{tan}\frac{\theta−\phi}{\mathrm{2}}\left(−{cos}^{\mathrm{2}} \frac{\theta+\phi}{\mathrm{2}}−{sin}^{\mathrm{2}} \frac{\theta+\phi}{\mathrm{2}}\right){i} \\ $$$$={itan}\frac{\theta−\phi}{\mathrm{2}} \\ $$
Commented by malwaan last updated on 01/Jan/19
no(ii)
$$\mathrm{no}\left(\mathrm{ii}\right) \\ $$
Commented by Tawa1 last updated on 01/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by $@ty@m last updated on 01/Jan/19
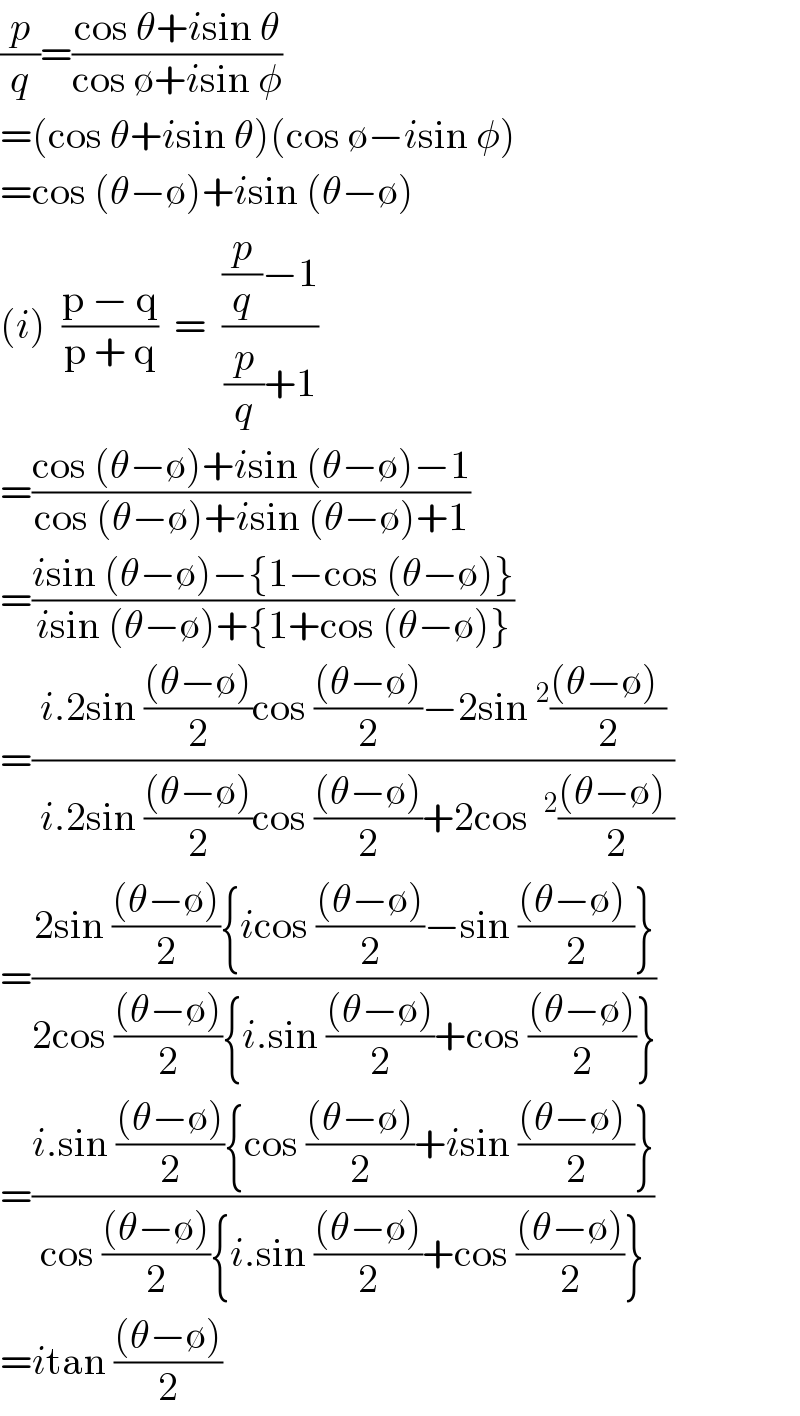
(p/q)=((cos θ+isin θ)/(cos ∅+isin φ)) =(cos θ+isin θ)(cos ∅−isin φ) =cos (θ−∅)+isin (θ−∅) (i) ((p − q)/(p + q)) = (((p/q)−1)/((p/q)+1)) =((cos (θ−∅)+isin (θ−∅)−1)/(cos (θ−∅)+isin (θ−∅)+1)) =((isin (θ−∅)−{1−cos (θ−∅)})/(isin (θ−∅)+{1+cos (θ−∅)})) =((i.2sin (((θ−∅))/2)cos (((θ−∅))/2)−2sin^2 (((θ−∅) )/2))/( i.2sin (((θ−∅))/2)cos (((θ−∅))/2)+2cos ^2 (((θ−∅) )/2))) =((2sin (((θ−∅))/2){icos (((θ−∅))/2)−sin (((θ−∅) )/2)})/(2cos (((θ−∅))/2){i.sin (((θ−∅))/2)+cos (((θ−∅))/2)})) =((i.sin (((θ−∅))/2){cos (((θ−∅))/2)+isin (((θ−∅) )/2)})/(cos (((θ−∅))/2){i.sin (((θ−∅))/2)+cos (((θ−∅))/2)})) =itan (((θ−∅))/2)
$$\frac{{p}}{{q}}=\frac{\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta}{\mathrm{cos}\:\emptyset+{i}\mathrm{sin}\:\phi} \\ $$$$=\left(\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta\right)\left(\mathrm{cos}\:\emptyset−{i}\mathrm{sin}\:\phi\right) \\ $$$$=\mathrm{cos}\:\left(\theta−\emptyset\right)+{i}\mathrm{sin}\:\left(\theta−\emptyset\right) \\ $$$$\left({i}\right)\:\:\frac{\mathrm{p}\:−\:\mathrm{q}}{\mathrm{p}\:+\:\mathrm{q}}\:\:=\:\:\frac{\frac{{p}}{{q}}−\mathrm{1}}{\frac{{p}}{{q}}+\mathrm{1}} \\ $$$$=\frac{\mathrm{cos}\:\left(\theta−\emptyset\right)+{i}\mathrm{sin}\:\left(\theta−\emptyset\right)−\mathrm{1}}{\mathrm{cos}\:\left(\theta−\emptyset\right)+{i}\mathrm{sin}\:\left(\theta−\emptyset\right)+\mathrm{1}} \\ $$$$=\frac{{i}\mathrm{sin}\:\left(\theta−\emptyset\right)−\left\{\mathrm{1}−\mathrm{cos}\:\left(\theta−\emptyset\right)\right\}}{{i}\mathrm{sin}\:\left(\theta−\emptyset\right)+\left\{\mathrm{1}+\mathrm{cos}\:\left(\theta−\emptyset\right)\right\}} \\ $$$$=\frac{{i}.\mathrm{2sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}−\mathrm{2sin}\:^{\mathrm{2}} \frac{\left(\theta−\emptyset\right)\:}{\mathrm{2}}}{\:{i}.\mathrm{2sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}+\mathrm{2cos}\:\:^{\mathrm{2}} \frac{\left(\theta−\emptyset\right)\:}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\left\{{i}\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}−\mathrm{sin}\:\frac{\left(\theta−\emptyset\right)\:}{\mathrm{2}}\right\}}{\mathrm{2cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\left\{{i}.\mathrm{sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}+\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\right\}} \\ $$$$=\frac{{i}.\mathrm{sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\left\{\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}+{i}\mathrm{sin}\:\frac{\left(\theta−\emptyset\right)\:}{\mathrm{2}}\right\}}{\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\left\{{i}.\mathrm{sin}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}+\mathrm{cos}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}}\right\}} \\ $$$$={i}\mathrm{tan}\:\frac{\left(\theta−\emptyset\right)}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 01/Jan/19
God bless you sir. Seen
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{Seen} \\ $$
Commented by $@ty@m last updated on 01/Jan/19
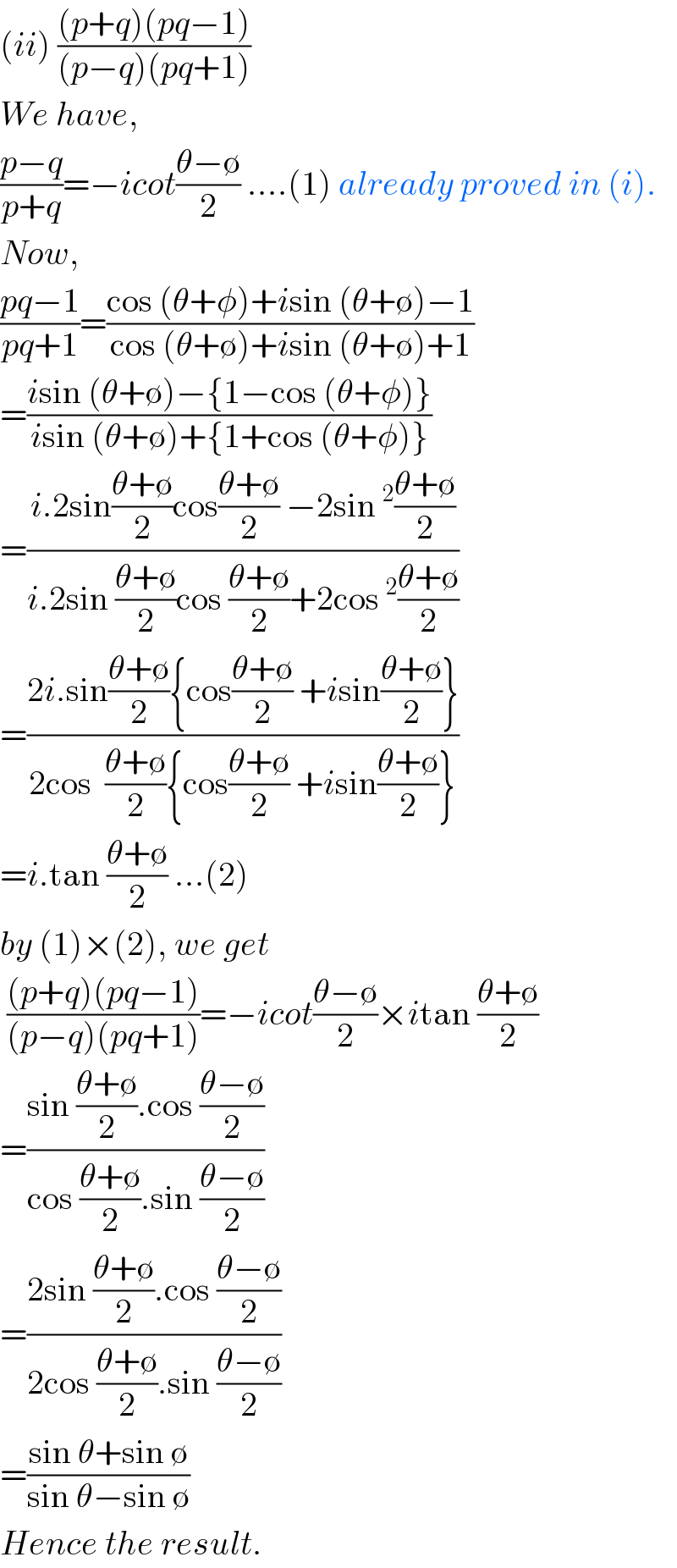
(ii) (((p+q)(pq−1))/((p−q)(pq+1))) We have, ((p−q)/(p+q))=−icot((θ−∅)/2) ....(1) already proved in (i). Now, ((pq−1)/(pq+1))=((cos (θ+φ)+isin (θ+∅)−1)/(cos (θ+∅)+isin (θ+∅)+1)) =((isin (θ+∅)−{1−cos (θ+φ)})/(isin (θ+∅)+{1+cos (θ+φ)})) =((i.2sin((θ+∅)/2)cos((θ+∅)/2) −2sin^2 ((θ+∅)/2))/(i.2sin ((θ+∅)/2)cos ((θ+∅)/2)+2cos^2 ((θ+∅)/2))) =((2i.sin((θ+∅)/2){cos((θ+∅)/2) +isin((θ+∅)/2)})/(2cos ((θ+∅)/2){cos((θ+∅)/2) +isin((θ+∅)/2)})) =i.tan ((θ+∅)/2) ...(2) by (1)×(2), we get (((p+q)(pq−1))/((p−q)(pq+1)))=−icot((θ−∅)/2)×itan ((θ+∅)/2) =((sin ((θ+∅)/2).cos ((θ−∅)/2))/(cos ((θ+∅)/2).sin ((θ−∅)/2))) =((2sin ((θ+∅)/2).cos ((θ−∅)/2))/(2cos ((θ+∅)/2).sin ((θ−∅)/2))) =((sin θ+sin ∅)/(sin θ−sin ∅)) Hence the result.
$$\left({ii}\right)\:\frac{\left({p}+{q}\right)\left({pq}−\mathrm{1}\right)}{\left({p}−{q}\right)\left({pq}+\mathrm{1}\right)} \\ $$$${We}\:{have}, \\ $$$$\frac{{p}−{q}}{{p}+{q}}=−{icot}\frac{\theta−\emptyset}{\mathrm{2}}\:….\left(\mathrm{1}\right)\:{already}\:{proved}\:{in}\:\left({i}\right). \\ $$$${Now}, \\ $$$$\frac{{pq}−\mathrm{1}}{{pq}+\mathrm{1}}=\frac{\mathrm{cos}\:\left(\theta+\phi\right)+{i}\mathrm{sin}\:\left(\theta+\emptyset\right)−\mathrm{1}}{\mathrm{cos}\:\left(\theta+\emptyset\right)+{i}\mathrm{sin}\:\left(\theta+\emptyset\right)+\mathrm{1}} \\ $$$$=\frac{{i}\mathrm{sin}\:\left(\theta+\emptyset\right)−\left\{\mathrm{1}−\mathrm{cos}\:\left(\theta+\phi\right)\right\}}{{i}\mathrm{sin}\:\left(\theta+\emptyset\right)+\left\{\mathrm{1}+\mathrm{cos}\:\left(\theta+\phi\right)\right\}} \\ $$$$=\frac{{i}.\mathrm{2sin}\frac{\theta+\emptyset}{\mathrm{2}}\mathrm{cos}\frac{\theta+\emptyset}{\mathrm{2}}\:−\mathrm{2sin}\:^{\mathrm{2}} \frac{\theta+\emptyset}{\mathrm{2}}}{{i}.\mathrm{2sin}\:\frac{\theta+\emptyset}{\mathrm{2}}\mathrm{cos}\:\frac{\theta+\emptyset}{\mathrm{2}}+\mathrm{2cos}\:^{\mathrm{2}} \frac{\theta+\emptyset}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2}{i}.\mathrm{sin}\frac{\theta+\emptyset}{\mathrm{2}}\left\{\mathrm{cos}\frac{\theta+\emptyset}{\mathrm{2}}\:+{i}\mathrm{sin}\frac{\theta+\emptyset}{\mathrm{2}}\right\}}{\mathrm{2cos}\:\:\frac{\theta+\emptyset}{\mathrm{2}}\left\{\mathrm{cos}\frac{\theta+\emptyset}{\mathrm{2}}\:+{i}\mathrm{sin}\frac{\theta+\emptyset}{\mathrm{2}}\right\}} \\ $$$$={i}.\mathrm{tan}\:\frac{\theta+\emptyset}{\mathrm{2}}\:…\left(\mathrm{2}\right) \\ $$$${by}\:\left(\mathrm{1}\right)×\left(\mathrm{2}\right),\:{we}\:{get} \\ $$$$\:\frac{\left({p}+{q}\right)\left({pq}−\mathrm{1}\right)}{\left({p}−{q}\right)\left({pq}+\mathrm{1}\right)}=−{icot}\frac{\theta−\emptyset}{\mathrm{2}}×{i}\mathrm{tan}\:\frac{\theta+\emptyset}{\mathrm{2}} \\ $$$$=\frac{\mathrm{sin}\:\frac{\theta+\emptyset}{\mathrm{2}}.\mathrm{cos}\:\frac{\theta−\emptyset}{\mathrm{2}}}{\mathrm{cos}\:\frac{\theta+\emptyset}{\mathrm{2}}.\mathrm{sin}\:\frac{\theta−\emptyset}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2sin}\:\frac{\theta+\emptyset}{\mathrm{2}}.\mathrm{cos}\:\frac{\theta−\emptyset}{\mathrm{2}}}{\mathrm{2cos}\:\frac{\theta+\emptyset}{\mathrm{2}}.\mathrm{sin}\:\frac{\theta−\emptyset}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{sin}\:\theta+\mathrm{sin}\:\emptyset}{\mathrm{sin}\:\theta−\mathrm{sin}\:\emptyset} \\ $$$${Hence}\:{the}\:{result}. \\ $$
Commented by $@ty@m last updated on 01/Jan/19
I was in hurry in the morning. So, there were few typing mistake crept in solution of (i), which I have corrected.
$${I}\:{was}\:{in}\:{hurry}\:{in}\:{the}\:{morning}.\:{So}, \\ $$$${there}\:{were}\:{few}\:{typing}\:{mistake}\:{crept} \\ $$$${in}\:{solution}\:{of}\:\left({i}\right),\:{which}\:{I}\:{have} \\ $$$${corrected}. \\ $$
Commented by peter frank last updated on 01/Jan/19
nice method sir
$${nice}\:{method}\:{sir} \\ $$
Commented by Tawa1 last updated on 01/Jan/19
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 01/Jan/19
Have tried but cannot simplify, please help if you have time sir
$$\mathrm{Have}\:\mathrm{tried}\:\mathrm{but}\:\mathrm{cannot}\:\mathrm{simplify},\:\mathrm{please}\:\mathrm{help}\:\mathrm{if}\:\mathrm{you}\:\mathrm{have}\:\mathrm{time}\:\mathrm{sir} \\ $$
Commented by $@ty@m last updated on 01/Jan/19
done above...
$${done}\:{above}… \\ $$
Commented by malwaan last updated on 05/Jan/19
thank you sir
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *