Question Number 58400 by rahul 19 last updated on 22/Apr/19
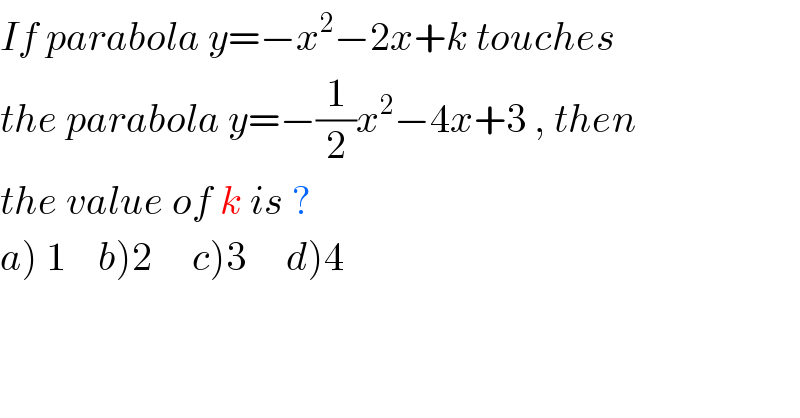
$${If}\:{parabola}\:{y}=−{x}^{\mathrm{2}} −\mathrm{2}{x}+{k}\:{touches} \\ $$$${the}\:{parabola}\:{y}=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\:,\:{then} \\ $$$${the}\:{value}\:{of}\:{k}\:{is}\:? \\ $$$$\left.{a}\left.\right)\left.\:\left.\mathrm{1}\:\:\:\:{b}\right)\mathrm{2}\:\:\:\:\:{c}\right)\mathrm{3}\:\:\:\:\:{d}\right)\mathrm{4} \\ $$
Commented by rahul 19 last updated on 22/Apr/19
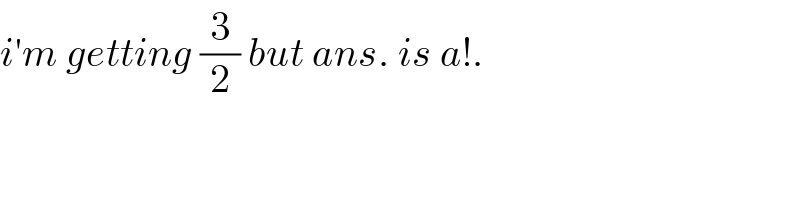
$${i}'{m}\:{getting}\:\frac{\mathrm{3}}{\mathrm{2}}\:{but}\:{ans}.\:{is}\:{a}!. \\ $$
Answered by mr W last updated on 22/Apr/19
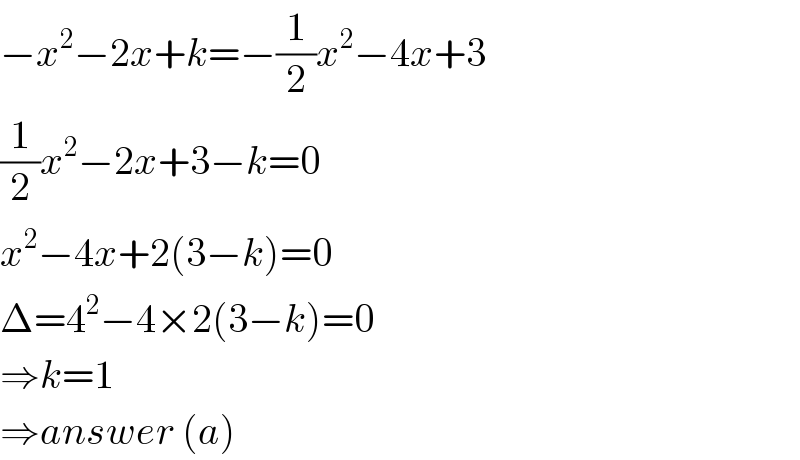
$$−{x}^{\mathrm{2}} −\mathrm{2}{x}+{k}=−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}−{k}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{2}\left(\mathrm{3}−{k}\right)=\mathrm{0} \\ $$$$\Delta=\mathrm{4}^{\mathrm{2}} −\mathrm{4}×\mathrm{2}\left(\mathrm{3}−{k}\right)=\mathrm{0} \\ $$$$\Rightarrow{k}=\mathrm{1} \\ $$$$\Rightarrow{answer}\:\left({a}\right) \\ $$
Commented by rahul 19 last updated on 23/Apr/19

$${thanks}\:{sir}! \\ $$
