Question Number 31147 by momo last updated on 03/Mar/18

Answered by ajfour last updated on 03/Mar/18
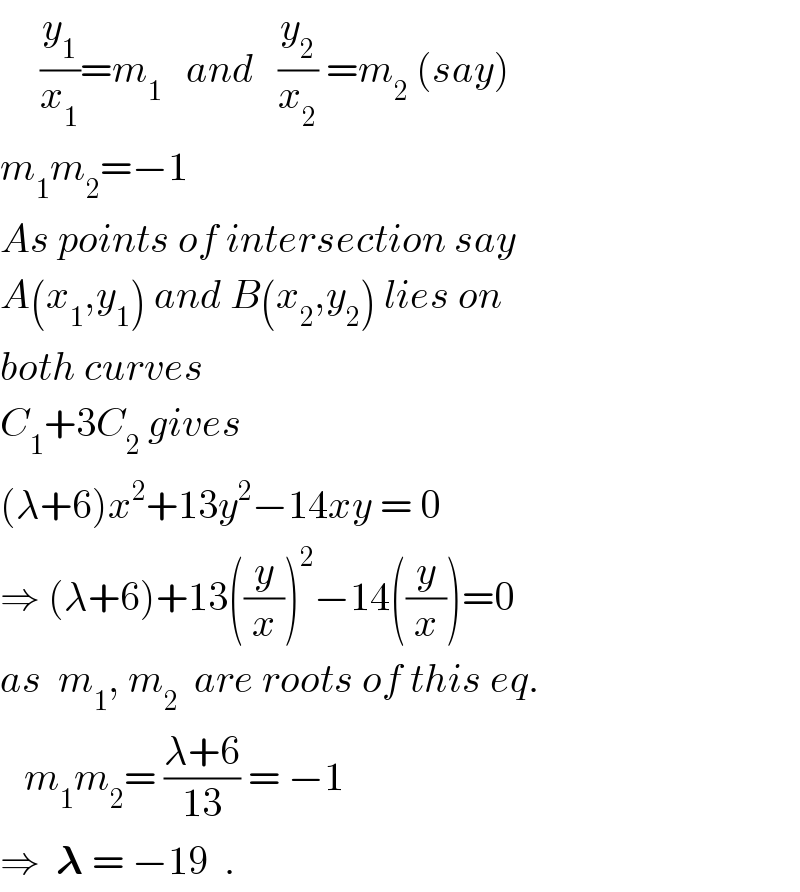
Commented by momo last updated on 03/Mar/18
Commented by momo last updated on 03/Mar/18
Commented by ajfour last updated on 03/Mar/18
Commented by ajfour last updated on 03/Mar/18

Commented by mrW2 last updated on 03/Mar/18
Ausgezeichnet!
Commented by mrW2 last updated on 03/Mar/18
Excellent! Outstanding!
Commented by ajfour last updated on 03/Mar/18