Question Number 166958 by cortano1 last updated on 03/Mar/22
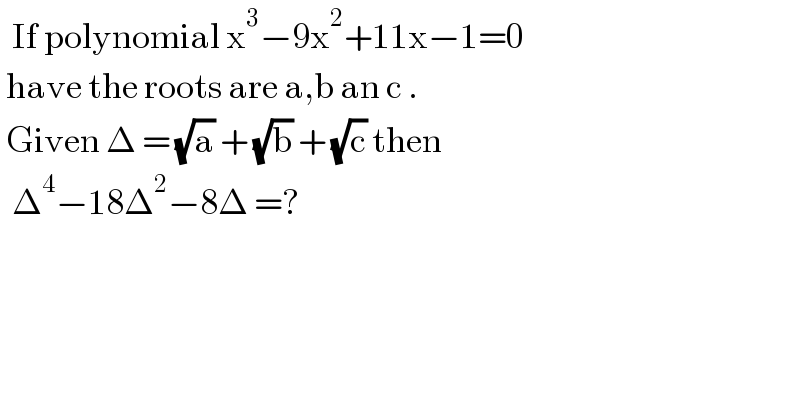
$$\:\:\mathrm{If}\:\mathrm{polynomial}\:\mathrm{x}^{\mathrm{3}} −\mathrm{9x}^{\mathrm{2}} +\mathrm{11x}−\mathrm{1}=\mathrm{0}\: \\ $$$$\:\mathrm{have}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{are}\:\mathrm{a},\mathrm{b}\:\mathrm{an}\:\mathrm{c}\:. \\ $$$$\:\mathrm{Given}\:\Delta\:=\:\sqrt{\mathrm{a}}\:+\:\sqrt{\mathrm{b}}\:+\:\sqrt{\mathrm{c}}\:\mathrm{then}\: \\ $$$$\:\:\Delta^{\mathrm{4}} −\mathrm{18}\Delta^{\mathrm{2}} −\mathrm{8}\Delta\:=? \\ $$$$ \\ $$
Commented by MJS_new last updated on 03/Mar/22

$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:−\mathrm{37} \\ $$$$ \\ $$$${x}^{\mathrm{3}} −\mathrm{9}{x}^{\mathrm{2}} +\mathrm{11}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{let}\:{x}={p}+\mathrm{3} \\ $$$${p}^{\mathrm{3}} −\mathrm{16}{p}−\mathrm{22}=\mathrm{0} \\ $$$$ \\ $$$$\Delta^{\mathrm{4}} −\mathrm{18}\Delta^{\mathrm{2}} −\mathrm{8}\Delta−\chi=\mathrm{0} \\ $$$$\left(\Delta^{\mathrm{2}} −\alpha\Delta−\beta\right)\left(\Delta^{\mathrm{2}} +\alpha\Delta−\gamma\right)=\mathrm{0} \\ $$$$\beta=−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{4}}{\alpha}+\mathrm{9}\wedge\gamma=−\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{4}}{\alpha}+\mathrm{9} \\ $$$$\alpha=\sqrt{{q}+\mathrm{12}} \\ $$$${q}^{\mathrm{3}} +\mathrm{4}\left(\chi−\mathrm{27}\right){q}+\mathrm{16}\left(\mathrm{3}\chi+\mathrm{23}\right)=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:\chi=−\mathrm{37}\:\Rightarrow\:{q}=\mathrm{4}{p} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{someone}\:\mathrm{else}\:\mathrm{please}\:\mathrm{explain}\:\mathrm{this};\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{fully}\:\mathrm{understand}\:\mathrm{what}\:\mathrm{I}\:\mathrm{did}… \\ $$
Answered by mr W last updated on 03/Mar/22
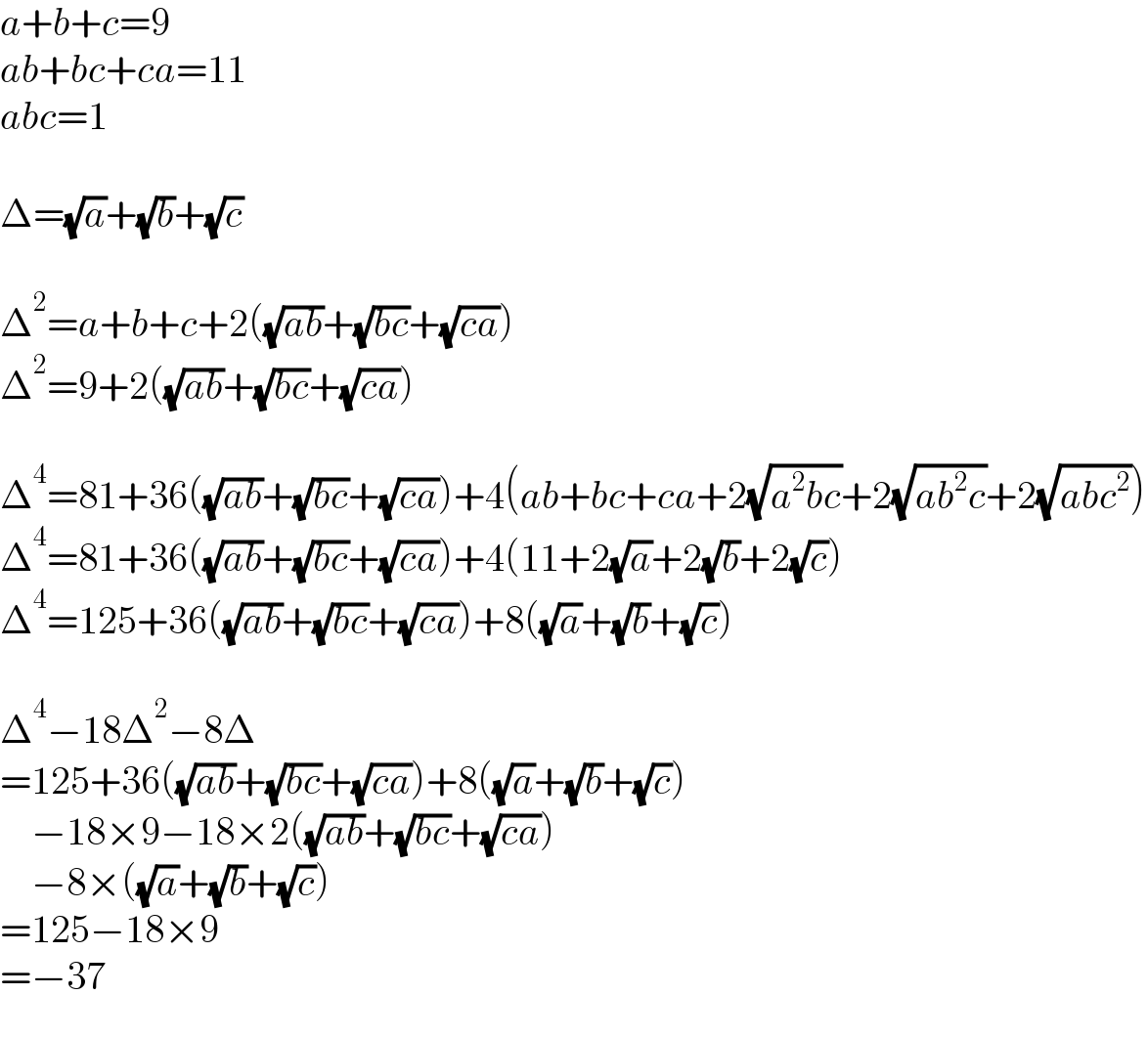
$${a}+{b}+{c}=\mathrm{9} \\ $$$${ab}+{bc}+{ca}=\mathrm{11} \\ $$$${abc}=\mathrm{1} \\ $$$$ \\ $$$$\Delta=\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}} \\ $$$$ \\ $$$$\Delta^{\mathrm{2}} ={a}+{b}+{c}+\mathrm{2}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right) \\ $$$$\Delta^{\mathrm{2}} =\mathrm{9}+\mathrm{2}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right) \\ $$$$ \\ $$$$\Delta^{\mathrm{4}} =\mathrm{81}+\mathrm{36}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right)+\mathrm{4}\left({ab}+{bc}+{ca}+\mathrm{2}\sqrt{{a}^{\mathrm{2}} {bc}}+\mathrm{2}\sqrt{{ab}^{\mathrm{2}} {c}}+\mathrm{2}\sqrt{{abc}^{\mathrm{2}} }\right) \\ $$$$\Delta^{\mathrm{4}} =\mathrm{81}+\mathrm{36}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right)+\mathrm{4}\left(\mathrm{11}+\mathrm{2}\sqrt{{a}}+\mathrm{2}\sqrt{{b}}+\mathrm{2}\sqrt{{c}}\right) \\ $$$$\Delta^{\mathrm{4}} =\mathrm{125}+\mathrm{36}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right)+\mathrm{8}\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right) \\ $$$$ \\ $$$$\Delta^{\mathrm{4}} −\mathrm{18}\Delta^{\mathrm{2}} −\mathrm{8}\Delta \\ $$$$=\mathrm{125}+\mathrm{36}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right)+\mathrm{8}\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right) \\ $$$$\:\:\:\:−\mathrm{18}×\mathrm{9}−\mathrm{18}×\mathrm{2}\left(\sqrt{{ab}}+\sqrt{{bc}}+\sqrt{{ca}}\right) \\ $$$$\:\:\:\:−\mathrm{8}×\left(\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\right) \\ $$$$=\mathrm{125}−\mathrm{18}×\mathrm{9} \\ $$$$=−\mathrm{37} \\ $$
Answered by null last updated on 03/Mar/22

$${upsilon} \\ $$
Answered by null last updated on 04/Mar/22

$$\mathrm{upsilon}=−\mathrm{37} \\ $$$$\upsilon=−\mathrm{37} \\ $$
