Question Number 43706 by Tawa1 last updated on 14/Sep/18
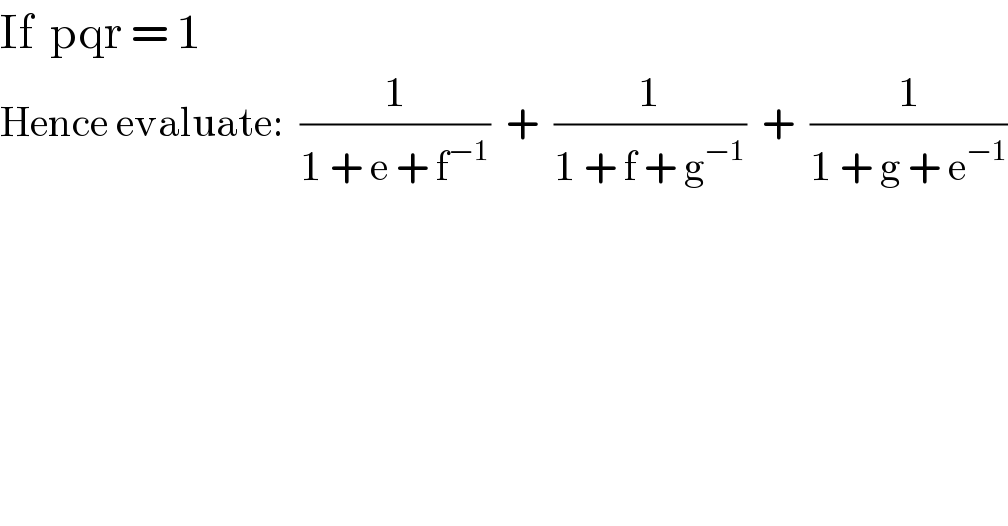
$$\mathrm{If}\:\:\mathrm{pqr}\:=\:\mathrm{1} \\ $$$$\mathrm{Hence}\:\mathrm{evaluate}:\:\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{e}\:+\:\mathrm{f}^{−\mathrm{1}} }\:\:+\:\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{f}\:+\:\mathrm{g}^{−\mathrm{1}} }\:\:+\:\:\frac{\mathrm{1}}{\mathrm{1}\:+\:\mathrm{g}\:+\:\mathrm{e}^{−\mathrm{1}} } \\ $$
Commented by Joel578 last updated on 14/Sep/18

$${p},{q},{r}\:\mathrm{and}\:{e},{f},{g}\:? \\ $$
Commented by Tawa1 last updated on 14/Sep/18
$$\mathrm{No}\:\mathrm{value}\:\mathrm{is}\:\mathrm{given}\:\mathrm{sir}.\:\mathrm{That}\:\mathrm{is}\:\mathrm{just}\:\mathrm{the}\:\mathrm{question} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Sep/18

$$\frac{\mathrm{1}}{\mathrm{1}+{p}+{q}^{−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{1}+{q}+{r}^{−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{1}+{r}+{p}^{−\mathrm{1}} } \\ $$$$\frac{{q}}{{q}+{pq}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+{q}+{pq}}+\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}+\frac{\mathrm{1}}{{p}}} \\ $$$$\frac{{q}}{{q}+{pq}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{1}+{q}+{pq}}+\frac{{pq}}{{pq}+\mathrm{1}+{q}} \\ $$$$=\frac{{q}+\mathrm{1}+{pq}}{{q}+{pq}+\mathrm{1}}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 14/Sep/18
$$\mathrm{wow},\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Meritguide1234 last updated on 15/Sep/18
$${you}\:{have}\:{solved}\:{different}\:{problem} \\ $$
Commented by Tawa1 last updated on 14/Sep/18
$$\mathrm{I}\:\mathrm{understand}.\:\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{correct}.\:\:\mathrm{God}\:\mathrm{bless}\:\mathrm{mr}\:\mathrm{tanmay} \\ $$
