Menu Close

If-secA-tanA-Q-than-prove-that-cosecA-1-Q-2-1-Q-2-

Tinku Tara 0 Comments
Pin




Question Number 173894 by azadsir last updated on 20/Jul/22
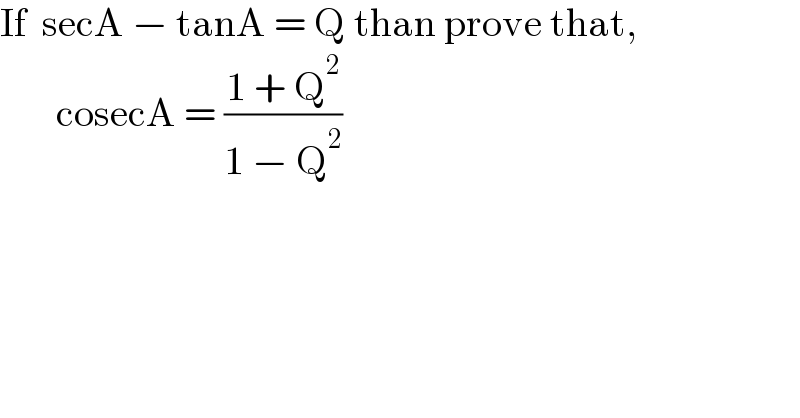
If secA − tanA = Q than prove that, cosecA = ((1 + Q^2 )/(1 − Q^2 ))
$$\mathrm{If}\:\:\mathrm{secA}\:−\:\mathrm{tanA}\:=\:\mathrm{Q}\:\mathrm{than}\:\mathrm{prove}\:\mathrm{that},\: \\ $$$$\:\:\:\:\:\:\:\mathrm{cosecA}\:=\:\frac{\mathrm{1}\:+\:\mathrm{Q}^{\mathrm{2}} }{\mathrm{1}\:−\:\mathrm{Q}^{\mathrm{2}} }\: \\ $$
Commented by cortano1 last updated on 20/Jul/22
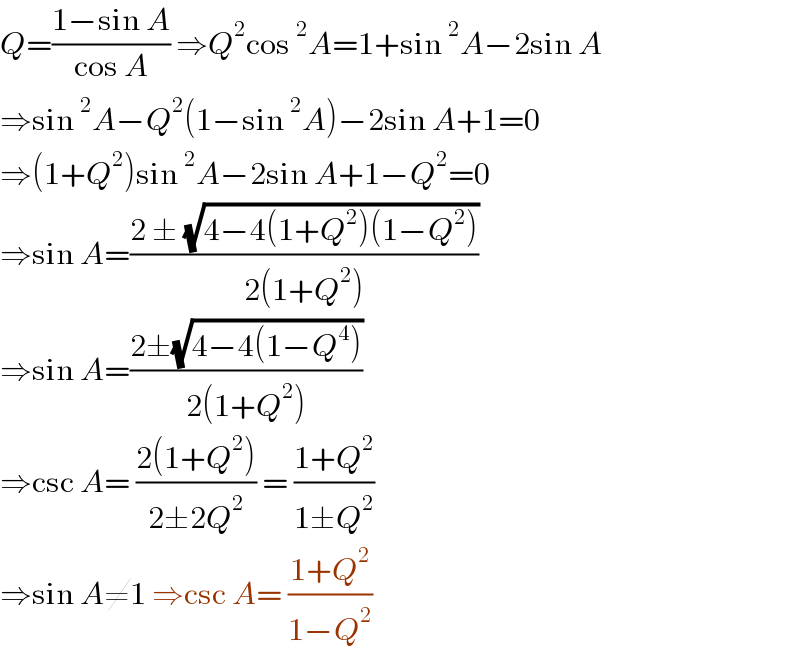
Q=((1−sin A)/(cos A)) ⇒Q^2 cos^2 A=1+sin^2 A−2sin A ⇒sin^2 A−Q^2 (1−sin^2 A)−2sin A+1=0 ⇒(1+Q^2 )sin^2 A−2sin A+1−Q^2 =0 ⇒sin A=((2 ± (√(4−4(1+Q^2 )(1−Q^2 ))))/(2(1+Q^2 ))) ⇒sin A=((2±(√(4−4(1−Q^4 ))))/(2(1+Q^2 ))) ⇒csc A= ((2(1+Q^2 ))/(2±2Q^2 )) = ((1+Q^2 )/(1±Q^2 )) ⇒sin A≠1 ⇒csc A= ((1+Q^2 )/(1−Q^2 ))
$${Q}=\frac{\mathrm{1}−\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}\:\Rightarrow{Q}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {A}=\mathrm{1}+\mathrm{sin}\:^{\mathrm{2}} {A}−\mathrm{2sin}\:{A} \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{2}} {A}−{Q}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {A}\right)−\mathrm{2sin}\:{A}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)\mathrm{sin}\:^{\mathrm{2}} {A}−\mathrm{2sin}\:{A}+\mathrm{1}−{Q}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:{A}=\frac{\mathrm{2}\:\pm\:\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)\left(\mathrm{1}−{Q}^{\mathrm{2}} \right)}}{\mathrm{2}\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{sin}\:{A}=\frac{\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}\left(\mathrm{1}−{Q}^{\mathrm{4}} \right)}}{\mathrm{2}\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)} \\ $$$$\Rightarrow\mathrm{csc}\:{A}=\:\frac{\mathrm{2}\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)}{\mathrm{2}\pm\mathrm{2}{Q}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}\pm{Q}^{\mathrm{2}} }\: \\ $$$$\Rightarrow\mathrm{sin}\:{A}\neq\mathrm{1}\:\Rightarrow\mathrm{csc}\:{A}=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} } \\ $$
Commented by azadsir last updated on 20/Jul/22
Thank you
$$\mathrm{Thank}\:\mathrm{you} \\ $$
Answered by blackmamba last updated on 20/Jul/22
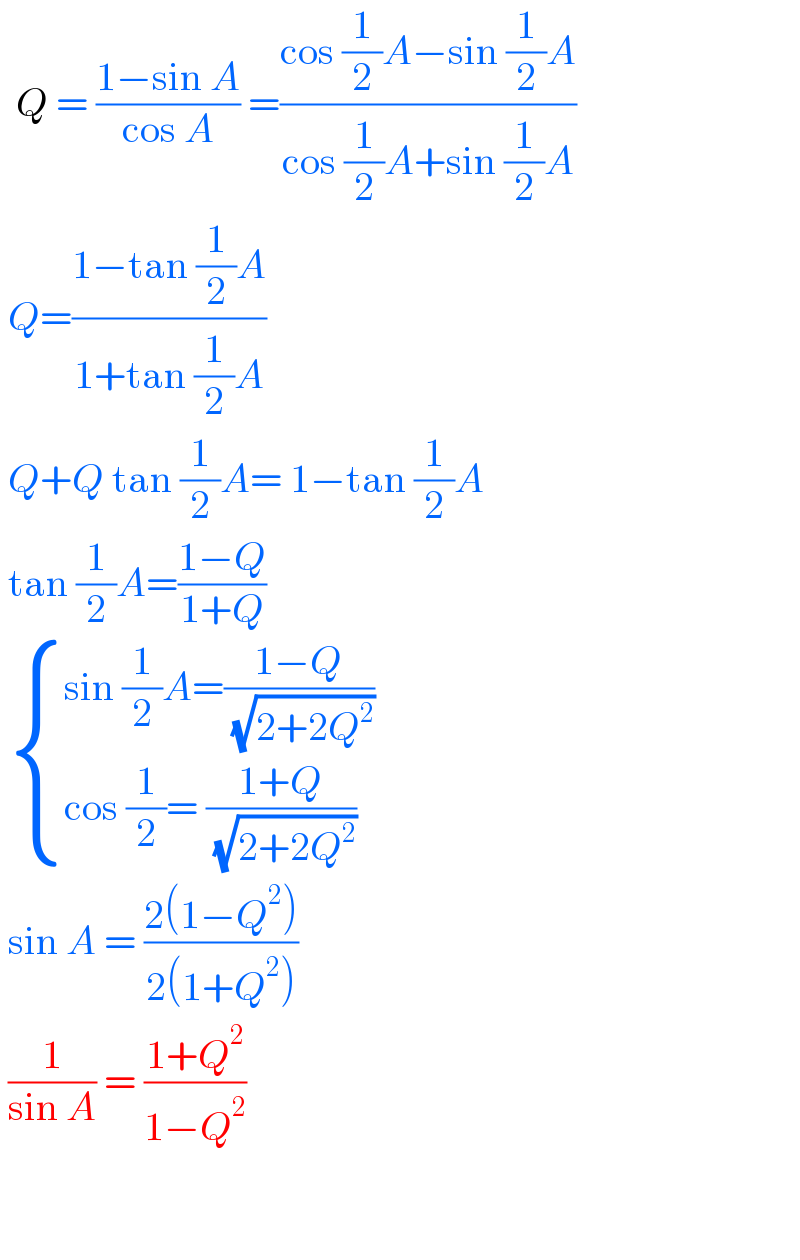
Q = ((1−sin A)/(cos A)) =((cos (1/2)A−sin (1/2)A)/(cos (1/2)A+sin (1/2)A)) Q=((1−tan (1/2)A)/(1+tan (1/2)A)) Q+Q tan (1/2)A= 1−tan (1/2)A tan (1/2)A=((1−Q)/(1+Q)) { ((sin (1/2)A=((1−Q)/( (√(2+2Q^2 )))))),((cos (1/2)= ((1+Q)/( (√(2+2Q^2 )))))) :} sin A = ((2(1−Q^2 ))/(2(1+Q^2 ))) (1/(sin A)) = ((1+Q^2 )/(1−Q^2 ))
$$\:\:{Q}\:=\:\frac{\mathrm{1}−\mathrm{sin}\:{A}}{\mathrm{cos}\:{A}}\:=\frac{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{A}−\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{A}}{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}{A}+\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{A}} \\ $$$$\:{Q}=\frac{\mathrm{1}−\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{A}}{\mathrm{1}+\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{A}} \\ $$$$\:{Q}+{Q}\:\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{A}=\:\mathrm{1}−\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{A} \\ $$$$\:\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}{A}=\frac{\mathrm{1}−{Q}}{\mathrm{1}+{Q}} \\ $$$$\:\begin{cases}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{A}=\frac{\mathrm{1}−{Q}}{\:\sqrt{\mathrm{2}+\mathrm{2}{Q}^{\mathrm{2}} }}}\\{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}=\:\frac{\mathrm{1}+{Q}}{\:\sqrt{\mathrm{2}+\mathrm{2}{Q}^{\mathrm{2}} }}}\end{cases} \\ $$$$\:\mathrm{sin}\:{A}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−{Q}^{\mathrm{2}} \right)}{\mathrm{2}\left(\mathrm{1}+{Q}^{\mathrm{2}} \right)} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{sin}\:{A}}\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} } \\ $$$$\: \\ $$$$\: \\ $$
Commented by azadsir last updated on 20/Jul/22
Thank you
$$\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by Tawa11 last updated on 21/Jul/22
Great sirs
$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by BaliramKumar last updated on 21/Jul/22
secA−tanA=Q ((1−sinA)/(cosA)) = Q (((1−sinA)^2 )/(cos^2 A)) = Q^2 (((1−sinA)^2 )/(1−sin^2 A)) = Q^2 (((1−sinA)^2 )/((1−sinA)(1+sinA))) = Q^2 (((1−sinA))/((1+sinA))) = Q^2 (((1+sinA))/((1−sinA))) = (1/Q^2 ) (((1+sinA)+(1−sinA))/((1+sinA)−(1−sinA))) = ((1+Q^2 )/(1−Q^2 )) [∵ If (a/b) = (c/d) then ((a+b)/(a−b)) = ((c+d)/(c−d)) ] (2/(2sinA)) = ((1+Q^2 )/(1−Q^2 )) (1/(sinA)) = ((1+Q^2 )/(1−Q^2 )) cosecA = ((1+Q^2 )/(1−Q^2 ))
$${secA}−{tanA}={Q} \\ $$$$\frac{\mathrm{1}−{sinA}}{{cosA}}\:=\:{Q} \\ $$$$\frac{\left(\mathrm{1}−{sinA}\right)^{\mathrm{2}} }{{cos}^{\mathrm{2}} {A}}\:=\:{Q}^{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}−{sinA}\right)^{\mathrm{2}} }{\mathrm{1}−{sin}^{\mathrm{2}} {A}}\:=\:{Q}^{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}−{sinA}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{sinA}\right)\left(\mathrm{1}+{sinA}\right)}\:=\:{Q}^{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}−{sinA}\right)}{\left(\mathrm{1}+{sinA}\right)}\:=\:{Q}^{\mathrm{2}} \\ $$$$\frac{\left(\mathrm{1}+{sinA}\right)}{\left(\mathrm{1}−{sinA}\right)}\:=\:\frac{\mathrm{1}}{{Q}^{\mathrm{2}} } \\ $$$$\frac{\left(\mathrm{1}+{sinA}\right)+\left(\mathrm{1}−{sinA}\right)}{\left(\mathrm{1}+{sinA}\right)−\left(\mathrm{1}−{sinA}\right)}\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} }\:\:\:\:\:\:\:\:\left[\because\:{If}\:\:\:\frac{{a}}{{b}}\:=\:\frac{{c}}{{d}}\:{then}\:\:\frac{{a}+{b}}{{a}−{b}}\:=\:\frac{{c}+{d}}{{c}−{d}}\:\:\right] \\ $$$$\frac{\mathrm{2}}{\mathrm{2}{sinA}}\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{sinA}}\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} } \\ $$$${cosecA}\:=\:\frac{\mathrm{1}+{Q}^{\mathrm{2}} }{\mathrm{1}−{Q}^{\mathrm{2}} }\:\:\:\:\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *