Question Number 100133 by bemath last updated on 25/Jun/20
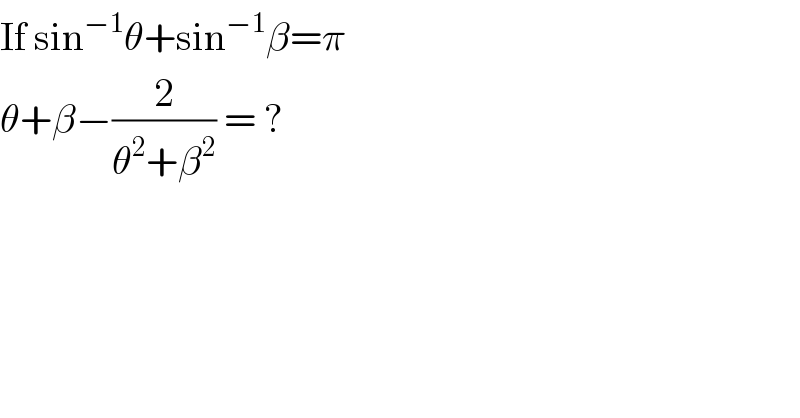
$$\mathrm{If}\:\mathrm{sin}^{−\mathrm{1}} \theta+\mathrm{sin}^{−\mathrm{1}} \beta=\pi\: \\ $$$$\theta+\beta−\frac{\mathrm{2}}{\theta^{\mathrm{2}} +\beta^{\mathrm{2}} }\:=\:? \\ $$
Answered by smridha last updated on 25/Jun/20
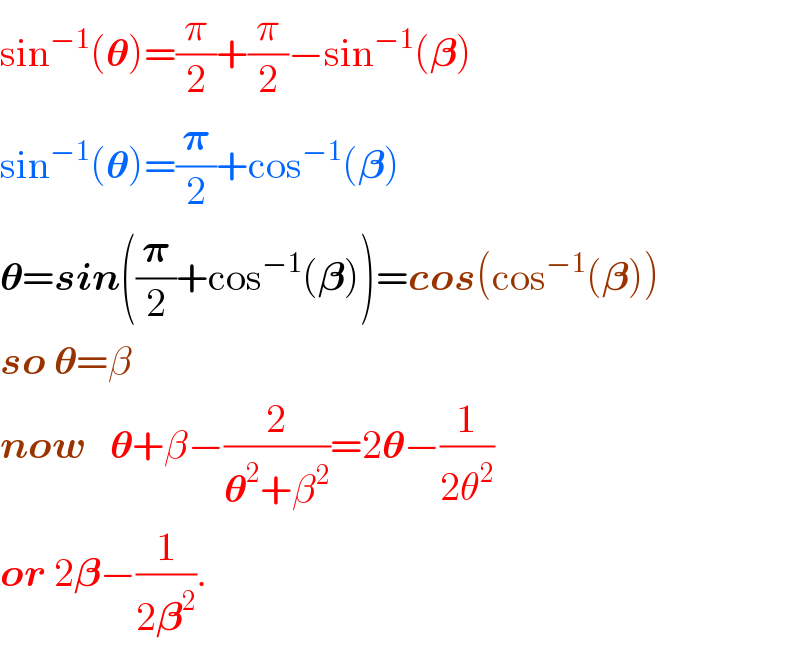
$$\mathrm{sin}^{−\mathrm{1}} \left(\boldsymbol{\theta}\right)=\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \left(\boldsymbol{\beta}\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\boldsymbol{\theta}\right)=\frac{\boldsymbol{\pi}}{\mathrm{2}}+\mathrm{cos}^{−\mathrm{1}} \left(\boldsymbol{\beta}\right) \\ $$$$\boldsymbol{\theta}=\boldsymbol{{sin}}\left(\frac{\boldsymbol{\pi}}{\mathrm{2}}+\mathrm{cos}^{−\mathrm{1}} \left(\boldsymbol{\beta}\right)\right)=\boldsymbol{{cos}}\left(\mathrm{cos}^{−\mathrm{1}} \left(\boldsymbol{\beta}\right)\right) \\ $$$$\boldsymbol{{so}}\:\boldsymbol{\theta}=\beta \\ $$$$\boldsymbol{{now}}\:\:\:\boldsymbol{\theta}+\beta−\frac{\mathrm{2}}{\boldsymbol{\theta}^{\mathrm{2}} +\beta^{\mathrm{2}} }=\mathrm{2}\boldsymbol{\theta}−\frac{\mathrm{1}}{\mathrm{2}\theta^{\mathrm{2}} } \\ $$$$\boldsymbol{{or}}\:\mathrm{2}\boldsymbol{\beta}−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\beta}^{\mathrm{2}} }. \\ $$
Commented by bemath last updated on 25/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{Mister} \\ $$
