Question Number 115328 by bobhans last updated on 25/Sep/20
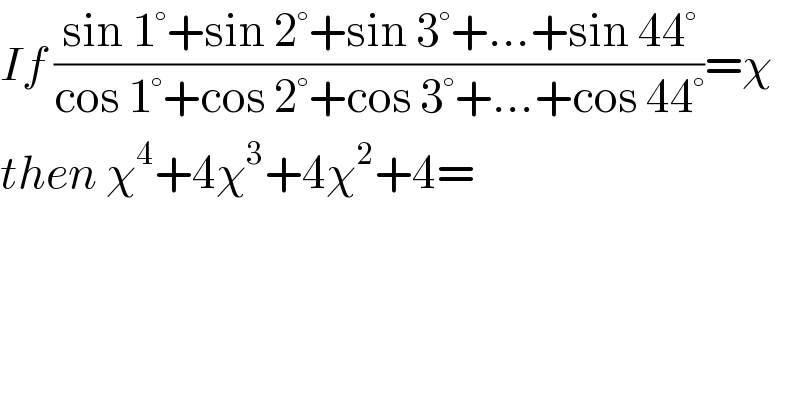
$${If}\:\frac{\mathrm{sin}\:\mathrm{1}°+\mathrm{sin}\:\mathrm{2}°+\mathrm{sin}\:\mathrm{3}°+…+\mathrm{sin}\:\mathrm{44}°}{\mathrm{cos}\:\mathrm{1}°+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{3}°+…+\mathrm{cos}\:\mathrm{44}°}=\chi \\ $$$${then}\:\chi^{\mathrm{4}} +\mathrm{4}\chi^{\mathrm{3}} +\mathrm{4}\chi^{\mathrm{2}} +\mathrm{4}= \\ $$
Answered by bemath last updated on 25/Sep/20
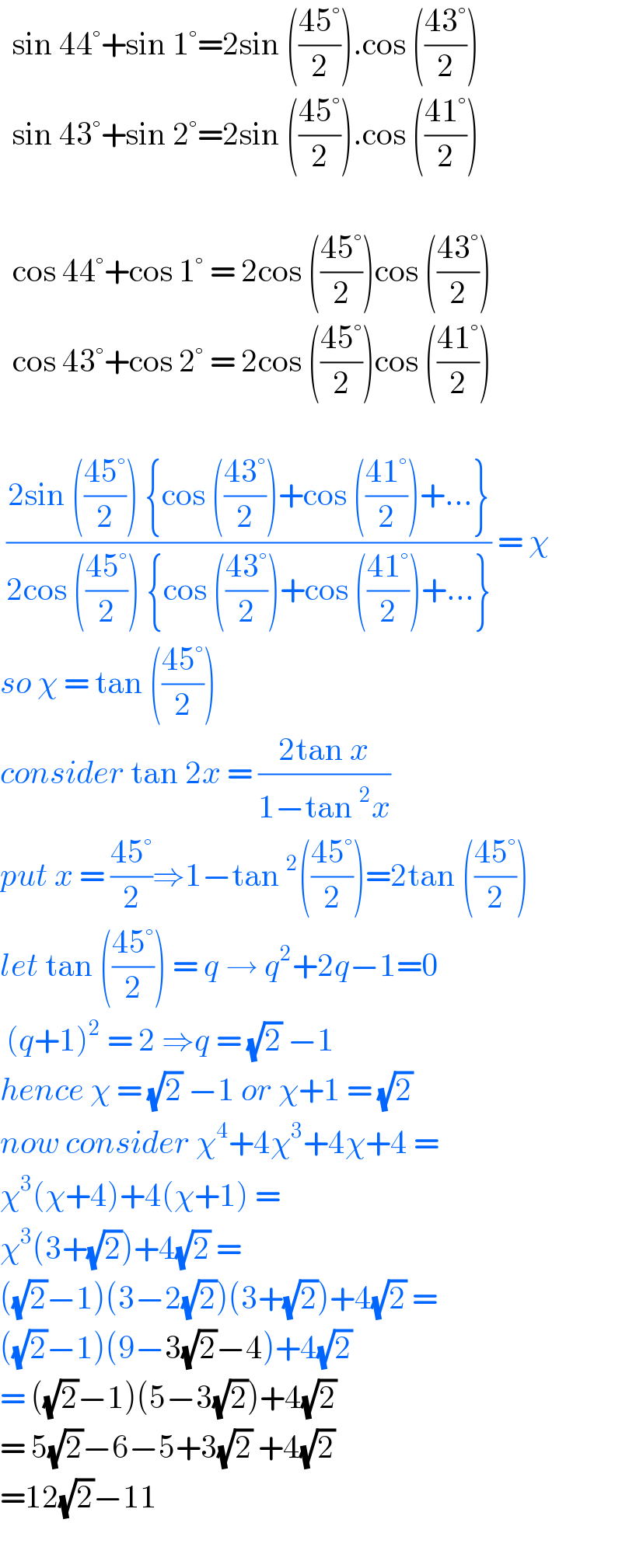
$$\:\:\mathrm{sin}\:\mathrm{44}°+\mathrm{sin}\:\mathrm{1}°=\mathrm{2sin}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right).\mathrm{cos}\:\left(\frac{\mathrm{43}°}{\mathrm{2}}\right) \\ $$$$\:\:\mathrm{sin}\:\mathrm{43}°+\mathrm{sin}\:\mathrm{2}°=\mathrm{2sin}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right).\mathrm{cos}\:\left(\frac{\mathrm{41}°}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\:\:\mathrm{cos}\:\mathrm{44}°+\mathrm{cos}\:\mathrm{1}°\:=\:\mathrm{2cos}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{43}°}{\mathrm{2}}\right) \\ $$$$\:\:\mathrm{cos}\:\mathrm{43}°+\mathrm{cos}\:\mathrm{2}°\:=\:\mathrm{2cos}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\mathrm{41}°}{\mathrm{2}}\right) \\ $$$$ \\ $$$$\:\frac{\mathrm{2sin}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)\:\left\{\mathrm{cos}\:\left(\frac{\mathrm{43}°}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{41}°}{\mathrm{2}}\right)+…\right\}}{\mathrm{2cos}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)\:\left\{\mathrm{cos}\:\left(\frac{\mathrm{43}°}{\mathrm{2}}\right)+\mathrm{cos}\:\left(\frac{\mathrm{41}°}{\mathrm{2}}\right)+…\right\}}\:=\:\chi \\ $$$${so}\:\chi\:=\:\mathrm{tan}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right) \\ $$$${consider}\:\mathrm{tan}\:\mathrm{2}{x}\:=\:\frac{\mathrm{2tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} {x}} \\ $$$${put}\:{x}\:=\:\frac{\mathrm{45}°}{\mathrm{2}}\Rightarrow\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{45}°}{\mathrm{2}}\right)=\mathrm{2tan}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right) \\ $$$${let}\:\mathrm{tan}\:\left(\frac{\mathrm{45}°}{\mathrm{2}}\right)\:=\:{q}\:\rightarrow\:{q}^{\mathrm{2}} +\mathrm{2}{q}−\mathrm{1}=\mathrm{0} \\ $$$$\:\left({q}+\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{2}\:\Rightarrow{q}\:=\:\sqrt{\mathrm{2}}\:−\mathrm{1} \\ $$$${hence}\:\chi\:=\:\sqrt{\mathrm{2}}\:−\mathrm{1}\:{or}\:\chi+\mathrm{1}\:=\:\sqrt{\mathrm{2}} \\ $$$${now}\:{consider}\:\chi^{\mathrm{4}} +\mathrm{4}\chi^{\mathrm{3}} +\mathrm{4}\chi+\mathrm{4}\:= \\ $$$$\chi^{\mathrm{3}} \left(\chi+\mathrm{4}\right)+\mathrm{4}\left(\chi+\mathrm{1}\right)\:= \\ $$$$\chi^{\mathrm{3}} \left(\mathrm{3}+\sqrt{\mathrm{2}}\right)+\mathrm{4}\sqrt{\mathrm{2}}\:=\: \\ $$$$\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{3}+\sqrt{\mathrm{2}}\right)+\mathrm{4}\sqrt{\mathrm{2}}\:= \\ $$$$\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{9}−\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{4}\right)+\mathrm{4}\sqrt{\mathrm{2}}\: \\ $$$$=\:\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\mathrm{5}−\mathrm{3}\sqrt{\mathrm{2}}\right)+\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$=\:\mathrm{5}\sqrt{\mathrm{2}}−\mathrm{6}−\mathrm{5}+\mathrm{3}\sqrt{\mathrm{2}}\:+\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$=\mathrm{12}\sqrt{\mathrm{2}}−\mathrm{11} \\ $$$$ \\ $$
