Menu Close

If-sin-2-x-cos-2-x-1-then-what-the-value-of-sin-11-x-cos-11-x-

Tinku Tara 0 Comments
Pin




Question Number 117257 by bemath last updated on 10/Oct/20
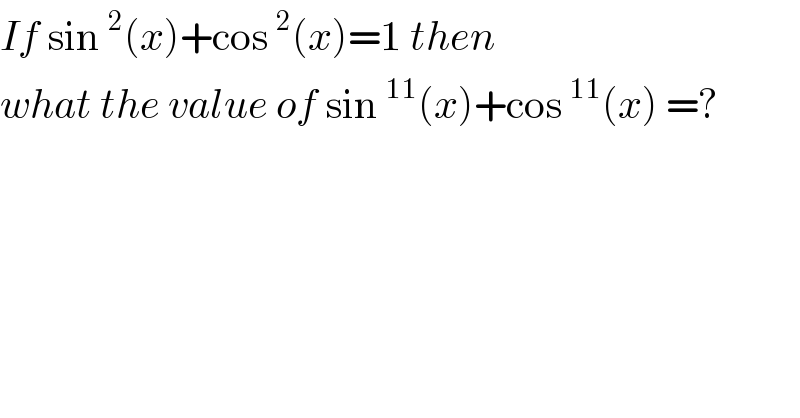
If sin^2 (x)+cos^2 (x)=1 then what the value of sin^(11) (x)+cos^(11) (x) =?
$${If}\:\mathrm{sin}\:^{\mathrm{2}} \left({x}\right)+\mathrm{cos}\:^{\mathrm{2}} \left({x}\right)=\mathrm{1}\:{then}\: \\ $$$${what}\:{the}\:{value}\:{of}\:\mathrm{sin}\:^{\mathrm{11}} \left({x}\right)+\mathrm{cos}\:^{\mathrm{11}} \left({x}\right)\:=? \\ $$
Commented by bemath last updated on 10/Oct/20
nice question
$$\mathrm{nice}\:\mathrm{question} \\ $$
Answered by mathmax by abdo last updated on 10/Oct/20
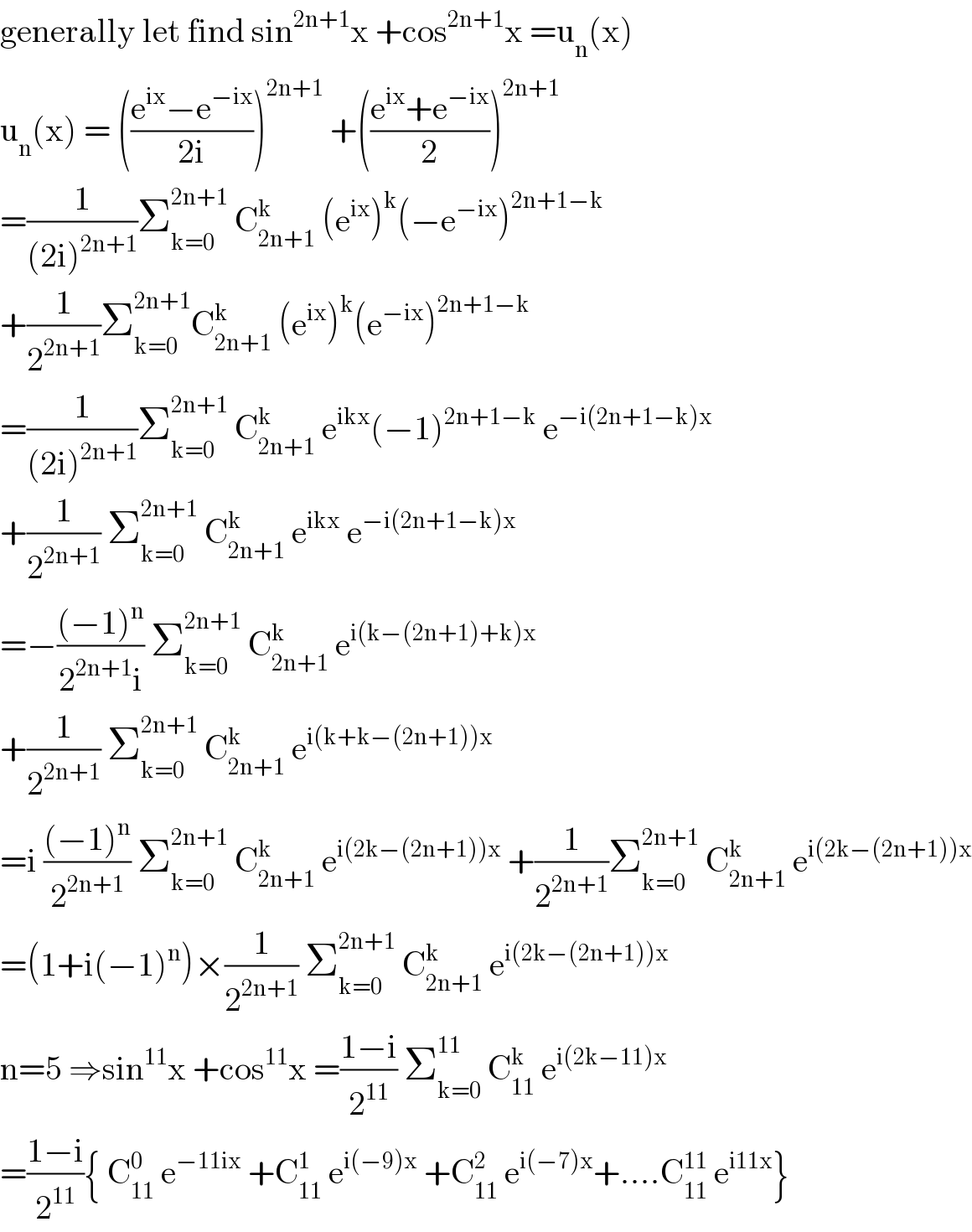
generally let find sin^(2n+1) x +cos^(2n+1) x =u_n (x) u_n (x) = (((e^(ix) −e^(−ix) )/(2i)))^(2n+1) +(((e^(ix) +e^(−ix) )/2))^(2n+1) =(1/((2i)^(2n+1) ))Σ_(k=0) ^(2n+1) C_(2n+1) ^k (e^(ix) )^k (−e^(−ix) )^(2n+1−k) +(1/2^(2n+1) )Σ_(k=0) ^(2n+1) C_(2n+1) ^k (e^(ix) )^k (e^(−ix) )^(2n+1−k) =(1/((2i)^(2n+1) ))Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(ikx) (−1)^(2n+1−k) e^(−i(2n+1−k)x) +(1/2^(2n+1) ) Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(ikx) e^(−i(2n+1−k)x) =−(((−1)^n )/(2^(2n+1) i)) Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(i(k−(2n+1)+k)x) +(1/2^(2n+1) ) Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(i(k+k−(2n+1))x) =i (((−1)^n )/2^(2n+1) ) Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(i(2k−(2n+1))x) +(1/2^(2n+1) )Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(i(2k−(2n+1))x) =(1+i(−1)^n )×(1/2^(2n+1) ) Σ_(k=0) ^(2n+1) C_(2n+1) ^k e^(i(2k−(2n+1))x) n=5 ⇒sin^(11) x +cos^(11) x =((1−i)/2^(11) ) Σ_(k=0) ^(11) C_(11) ^k e^(i(2k−11)x) =((1−i)/2^(11) ){ C_(11) ^0 e^(−11ix) +C_(11) ^1 e^(i(−9)x) +C_(11) ^2 e^(i(−7)x) +....C_(11) ^(11) e^(i11x) }
$$\mathrm{generally}\:\mathrm{let}\:\mathrm{find}\:\mathrm{sin}^{\mathrm{2n}+\mathrm{1}} \mathrm{x}\:+\mathrm{cos}^{\mathrm{2n}+\mathrm{1}} \mathrm{x}\:=\mathrm{u}_{\mathrm{n}} \left(\mathrm{x}\right) \\ $$$$\mathrm{u}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\:\left(\frac{\mathrm{e}^{\mathrm{ix}} −\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2i}}\right)^{\mathrm{2n}+\mathrm{1}} \:+\left(\frac{\mathrm{e}^{\mathrm{ix}} +\mathrm{e}^{−\mathrm{ix}} }{\mathrm{2}}\right)^{\mathrm{2n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{2n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(−\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{2n}+\mathrm{1}−\mathrm{k}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\left(\mathrm{e}^{\mathrm{ix}} \right)^{\mathrm{k}} \left(\mathrm{e}^{−\mathrm{ix}} \right)^{\mathrm{2n}+\mathrm{1}−\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2i}\right)^{\mathrm{2n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \left(−\mathrm{1}\right)^{\mathrm{2n}+\mathrm{1}−\mathrm{k}} \:\mathrm{e}^{−\mathrm{i}\left(\mathrm{2n}+\mathrm{1}−\mathrm{k}\right)\mathrm{x}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{ikx}} \:\mathrm{e}^{−\mathrm{i}\left(\mathrm{2n}+\mathrm{1}−\mathrm{k}\right)\mathrm{x}} \\ $$$$=−\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} \mathrm{i}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{k}−\left(\mathrm{2n}+\mathrm{1}\right)+\mathrm{k}\right)\mathrm{x}} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{k}+\mathrm{k}−\left(\mathrm{2n}+\mathrm{1}\right)\right)\mathrm{x}} \\ $$$$=\mathrm{i}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\left(\mathrm{2n}+\mathrm{1}\right)\right)\mathrm{x}} \:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\left(\mathrm{2n}+\mathrm{1}\right)\right)\mathrm{x}} \\ $$$$=\left(\mathrm{1}+\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{n}} \right)×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2n}+\mathrm{1}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}+\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}+\mathrm{1}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\left(\mathrm{2n}+\mathrm{1}\right)\right)\mathrm{x}} \\ $$$$\mathrm{n}=\mathrm{5}\:\Rightarrow\mathrm{sin}^{\mathrm{11}} \mathrm{x}\:+\mathrm{cos}^{\mathrm{11}} \mathrm{x}\:=\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}^{\mathrm{11}} }\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{11}} \:\mathrm{C}_{\mathrm{11}} ^{\mathrm{k}} \:\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}−\mathrm{11}\right)\mathrm{x}} \\ $$$$=\frac{\mathrm{1}−\mathrm{i}}{\mathrm{2}^{\mathrm{11}} }\left\{\:\mathrm{C}_{\mathrm{11}} ^{\mathrm{0}} \:\mathrm{e}^{−\mathrm{11ix}} \:+\mathrm{C}_{\mathrm{11}} ^{\mathrm{1}} \:\mathrm{e}^{\mathrm{i}\left(−\mathrm{9}\right)\mathrm{x}} \:+\mathrm{C}_{\mathrm{11}} ^{\mathrm{2}} \:\mathrm{e}^{\mathrm{i}\left(−\mathrm{7}\right)\mathrm{x}} +….\mathrm{C}_{\mathrm{11}} ^{\mathrm{11}} \:\mathrm{e}^{\mathrm{i11x}} \right\} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *