Question Number 78709 by jagoll last updated on 20/Jan/20
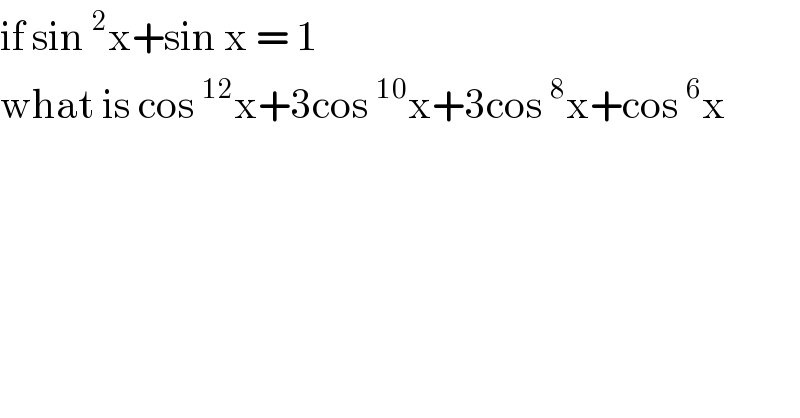
$$\mathrm{if}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{1} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{cos}\:^{\mathrm{12}} \mathrm{x}+\mathrm{3cos}\:^{\mathrm{10}} \mathrm{x}+\mathrm{3cos}\:^{\mathrm{8}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{x} \\ $$
Commented by jagoll last updated on 20/Jan/20
$$\mathrm{thanks}\:\mathrm{sir}\:\mathrm{john}\:\mathrm{and}\:\mathrm{sir}\:\mathrm{som} \\ $$
Answered by john santu last updated on 20/Jan/20

Commented by john santu last updated on 20/Jan/20

$${edit}\::\:\mathrm{cos}\:^{\mathrm{6}} {x}=\left(\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)×\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\mathrm{5}}−\mathrm{2} \\ $$$$\therefore\:\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)\left\{\sqrt{\mathrm{5}}−\mathrm{2}+\frac{\mathrm{9}−\mathrm{3}\sqrt{\mathrm{5}}+\mathrm{3}\sqrt{\mathrm{5}}−\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right\}= \\ $$$$\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)\left(\sqrt{\mathrm{5}}−\mathrm{1}+\frac{\mathrm{6}}{\mathrm{2}}\right)\:=\: \\ $$$$\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)\left(\sqrt{\mathrm{5}}+\mathrm{2}\right)=\mathrm{5}−\mathrm{4}\:=\mathrm{1}\:\bigstar \\ $$
Answered by som(math1967) last updated on 20/Jan/20
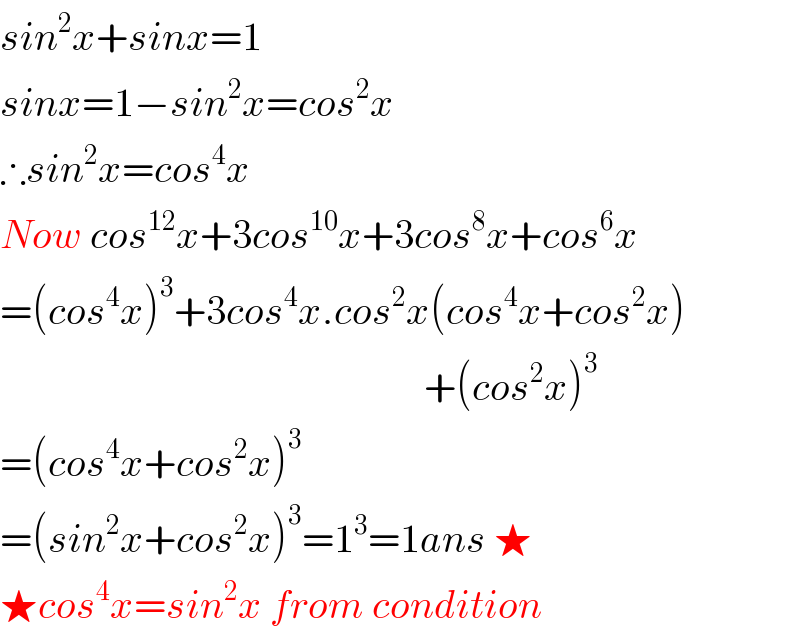
$${sin}^{\mathrm{2}} {x}+{sinx}=\mathrm{1} \\ $$$${sinx}=\mathrm{1}−{sin}^{\mathrm{2}} {x}={cos}^{\mathrm{2}} {x} \\ $$$$\therefore{sin}^{\mathrm{2}} {x}={cos}^{\mathrm{4}} {x} \\ $$$${Now}\:{cos}^{\mathrm{12}} {x}+\mathrm{3}{cos}^{\mathrm{10}} {x}+\mathrm{3}{cos}^{\mathrm{8}} {x}+{cos}^{\mathrm{6}} {x} \\ $$$$=\left({cos}^{\mathrm{4}} {x}\right)^{\mathrm{3}} +\mathrm{3}{cos}^{\mathrm{4}} {x}.{cos}^{\mathrm{2}} {x}\left({cos}^{\mathrm{4}} {x}+{cos}^{\mathrm{2}} {x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \\ $$$$=\left({cos}^{\mathrm{4}} {x}+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \\ $$$$=\left({sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} =\mathrm{1}^{\mathrm{3}} =\mathrm{1}{ans}\:\bigstar \\ $$$$\bigstar{cos}^{\mathrm{4}} {x}={sin}^{\mathrm{2}} {x}\:{from}\:{condition} \\ $$
