Menu Close

If-sin-2cos-1-then-2sin-cos-

Tinku Tara 0 Comments
Pin




Question Number 124309 by bemath last updated on 02/Dec/20
If sin θ+2cos θ=1 ; then 2sin θ−cos θ=?
Ifsinθ+2cosθ=1;then2sinθ−cosθ=?
Answered by MJS_new last updated on 02/Dec/20
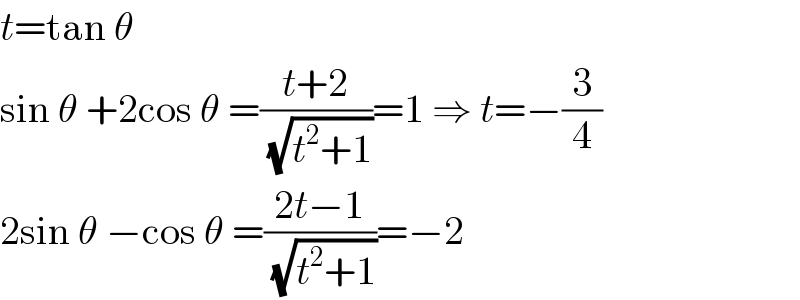
t=tan θ sin θ +2cos θ =((t+2)/( (√(t^2 +1))))=1 ⇒ t=−(3/4) 2sin θ −cos θ =((2t−1)/( (√(t^2 +1))))=−2
t=tanθsinθ+2cosθ=t+2t2+1=1⇒t=−342sinθ−cosθ=2t−1t2+1=−2
Answered by liberty last updated on 02/Dec/20
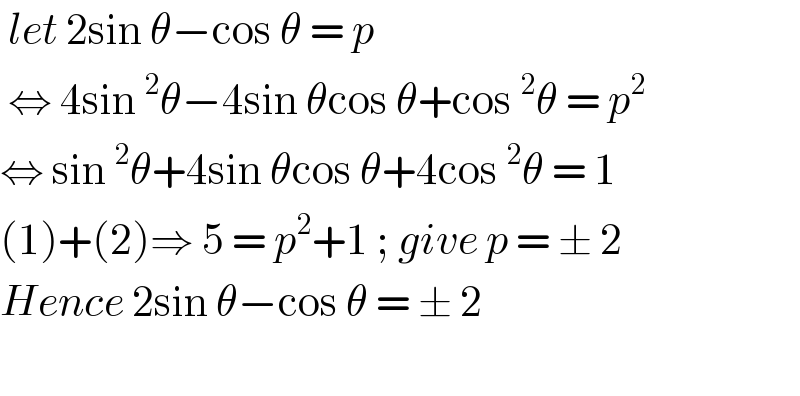
let 2sin θ−cos θ = p ⇔ 4sin^2 θ−4sin θcos θ+cos^2 θ = p^2 ⇔ sin^2 θ+4sin θcos θ+4cos^2 θ = 1 (1)+(2)⇒ 5 = p^2 +1 ; give p = ± 2 Hence 2sin θ−cos θ = ± 2
let2sinθ−cosθ=p⇔4sin2θ−4sinθcosθ+cos2θ=p2⇔sin2θ+4sinθcosθ+4cos2θ=1(1)+(2)⇒5=p2+1;givep=±2Hence2sinθ−cosθ=±2
Answered by Dwaipayan Shikari last updated on 02/Dec/20
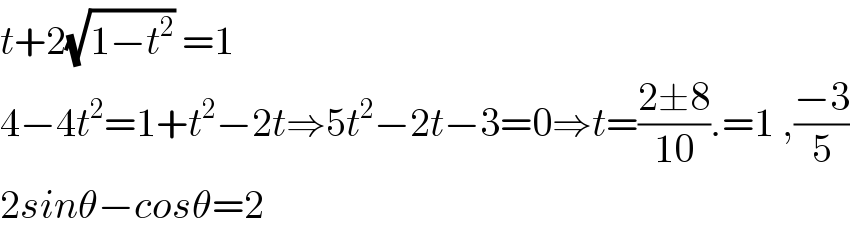
t+2(√(1−t^2 )) =1 4−4t^2 =1+t^2 −2t⇒5t^2 −2t−3=0⇒t=((2±8)/(10)).=1 ,((−3)/5) 2sinθ−cosθ=2
t+21−t2=14−4t2=1+t2−2t⇒5t2−2t−3=0⇒t=2±810.=1,−352sinθ−cosθ=2
Commented by bemath last updated on 02/Dec/20
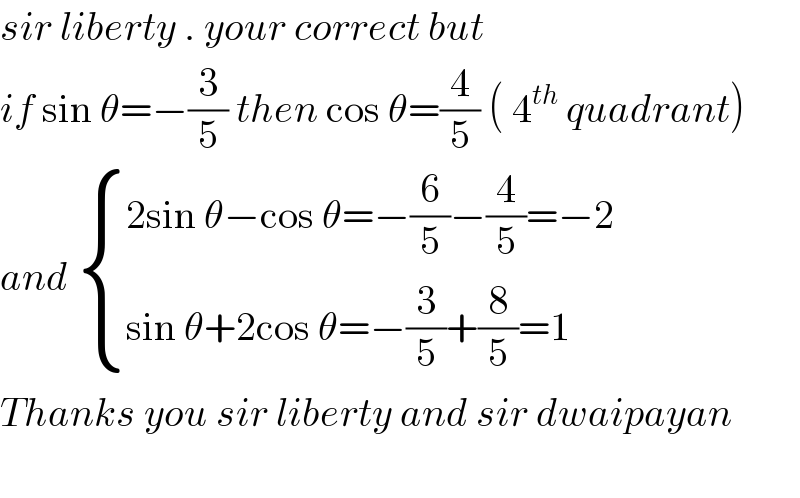
sir liberty . your correct but if sin θ=−(3/5) then cos θ=(4/5) ( 4^(th) quadrant) and { ((2sin θ−cos θ=−(6/5)−(4/5)=−2)),((sin θ+2cos θ=−(3/5)+(8/5)=1)) :} Thanks you sir liberty and sir dwaipayan
sirliberty.yourcorrectbutifsinθ=−35thencosθ=45(4thquadrant)and{2sinθ−cosθ=−65−45=−2sinθ+2cosθ=−35+85=1Thanksyousirlibertyandsirdwaipayan
Commented by liberty last updated on 02/Dec/20
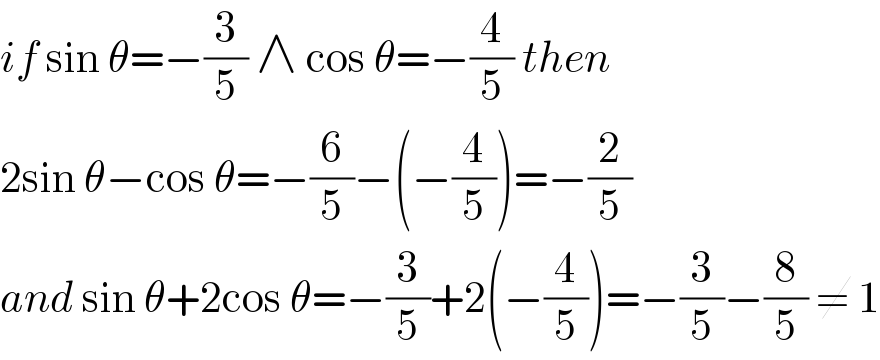
if sin θ=−(3/5) ∧ cos θ=−(4/5) then 2sin θ−cos θ=−(6/5)−(−(4/5))=−(2/5) and sin θ+2cos θ=−(3/5)+2(−(4/5))=−(3/5)−(8/5) ≠ 1
ifsinθ=−35∧cosθ=−45then2sinθ−cosθ=−65−(−45)=−25andsinθ+2cosθ=−35+2(−45)=−35−85≠1
Commented by Dwaipayan Shikari last updated on 02/Dec/20
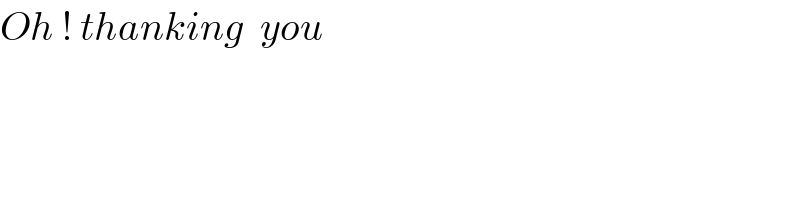
Oh ! thanking you
Oh!thankingyou
Answered by Dwaipayan Shikari last updated on 02/Dec/20
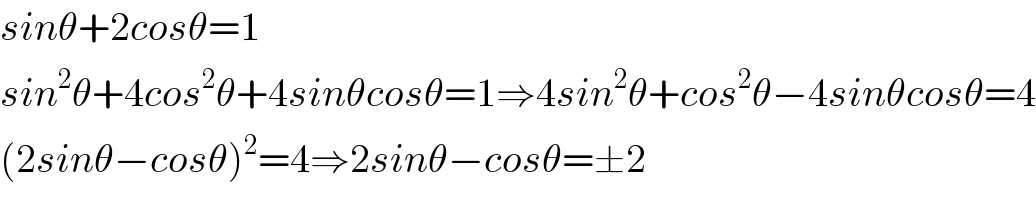
sinθ+2cosθ=1 sin^2 θ+4cos^2 θ+4sinθcosθ=1⇒4sin^2 θ+cos^2 θ−4sinθcosθ=4 (2sinθ−cosθ)^2 =4⇒2sinθ−cosθ=±2
sinθ+2cosθ=1sin2θ+4cos2θ+4sinθcosθ=1⇒4sin2θ+cos2θ−4sinθcosθ=4(2sinθ−cosθ)2=4⇒2sinθ−cosθ=±2

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *