If-sin-3-cos-3-x-sin-cos-y-then-find-a-relationship-between-x-y-indepentent-of-

Question Number 164945 by mnjuly1970 last updated on 23/Jan/22

If { (( sin ( 3θ ) + cos ( 3θ ) = x)),(( sin( θ ) + cos (θ ) = y)) :} then , find a relationship between x , y indepentent of , θ .

$$ \\ $$$$\:\:\mathrm{I}{f}\:\:\:\begin{cases}{\:\:{sin}\:\left(\:\mathrm{3}\theta\:\right)\:+\:{cos}\:\left(\:\mathrm{3}\theta\:\right)\:=\:{x}}\\{\:\:\:\:\:{sin}\left(\:\theta\:\right)\:+\:{cos}\:\left(\theta\:\right)\:=\:{y}}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:{then}\:\:,\:{find}\:\:{a}\:{relationship}\: \\ $$$$\:\:\:\:\:\:\:\:{between}\:\:\:{x}\:\:,\:\:{y}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:{indepentent}\:{of}\:,\:\:\:\theta\:. \\ $$

Answered by mr W last updated on 23/Jan/22

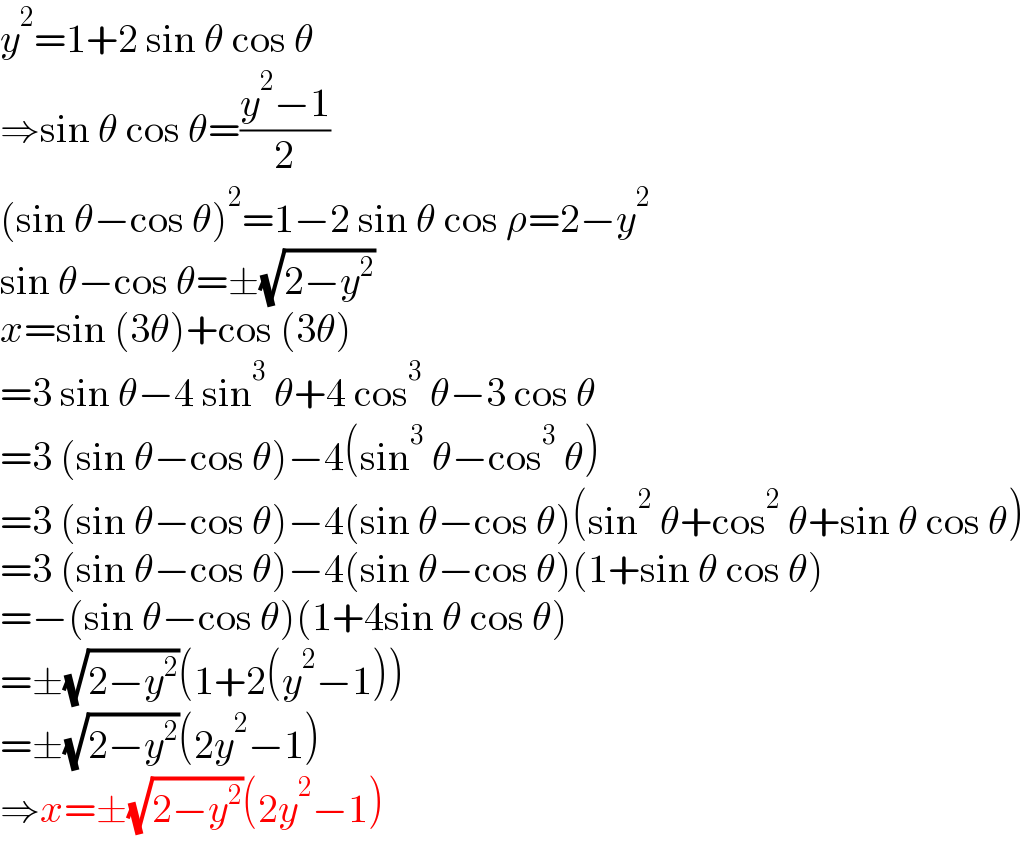
y^2 =1+2 sin θ cos θ ⇒sin θ cos θ=((y^2 −1)/2) (sin θ−cos θ)^2 =1−2 sin θ cos ρ=2−y^2 sin θ−cos θ=±(√(2−y^2 )) x=sin (3θ)+cos (3θ) =3 sin θ−4 sin^3 θ+4 cos^3 θ−3 cos θ =3 (sin θ−cos θ)−4(sin^3 θ−cos^3 θ) =3 (sin θ−cos θ)−4(sin θ−cos θ)(sin^2 θ+cos^2 θ+sin θ cos θ) =3 (sin θ−cos θ)−4(sin θ−cos θ)(1+sin θ cos θ) =−(sin θ−cos θ)(1+4sin θ cos θ) =±(√(2−y^2 ))(1+2(y^2 −1)) =±(√(2−y^2 ))(2y^2 −1) ⇒x=±(√(2−y^2 ))(2y^2 −1)

$${y}^{\mathrm{2}} =\mathrm{1}+\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\Rightarrow\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta=\frac{{y}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\mathrm{1}−\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\rho=\mathrm{2}−{y}^{\mathrm{2}} \\ $$$$\mathrm{sin}\:\theta−\mathrm{cos}\:\theta=\pm\sqrt{\mathrm{2}−{y}^{\mathrm{2}} } \\ $$$${x}=\mathrm{sin}\:\left(\mathrm{3}\theta\right)+\mathrm{cos}\:\left(\mathrm{3}\theta\right) \\ $$$$=\mathrm{3}\:\mathrm{sin}\:\theta−\mathrm{4}\:\mathrm{sin}^{\mathrm{3}} \:\theta+\mathrm{4}\:\mathrm{cos}^{\mathrm{3}} \:\theta−\mathrm{3}\:\mathrm{cos}\:\theta \\ $$$$=\mathrm{3}\:\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)−\mathrm{4}\left(\mathrm{sin}^{\mathrm{3}} \:\theta−\mathrm{cos}^{\mathrm{3}} \:\theta\right) \\ $$$$=\mathrm{3}\:\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)−\mathrm{4}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)\left(\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right) \\ $$$$=\mathrm{3}\:\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)−\mathrm{4}\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\right) \\ $$$$=−\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)\left(\mathrm{1}+\mathrm{4sin}\:\theta\:\mathrm{cos}\:\theta\right) \\ $$$$=\pm\sqrt{\mathrm{2}−{y}^{\mathrm{2}} }\left(\mathrm{1}+\mathrm{2}\left({y}^{\mathrm{2}} −\mathrm{1}\right)\right) \\ $$$$=\pm\sqrt{\mathrm{2}−{y}^{\mathrm{2}} }\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\right) \\ $$$$\Rightarrow{x}=\pm\sqrt{\mathrm{2}−{y}^{\mathrm{2}} }\left(\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\right) \\ $$

Commented by mnjuly1970 last updated on 23/Jan/22

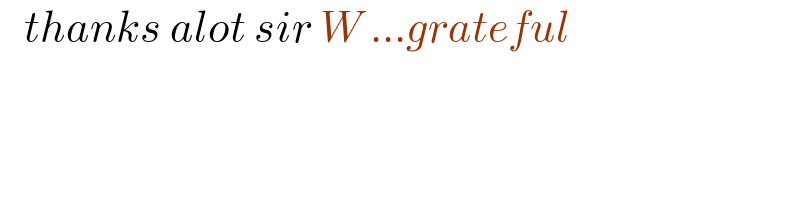
$$\:\:\:{thanks}\:{alot}\:{sir}\:{W}\:…{grateful} \\ $$

Commented by Tawa11 last updated on 23/Jan/22

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Answered by TheSupreme last updated on 24/Jan/22

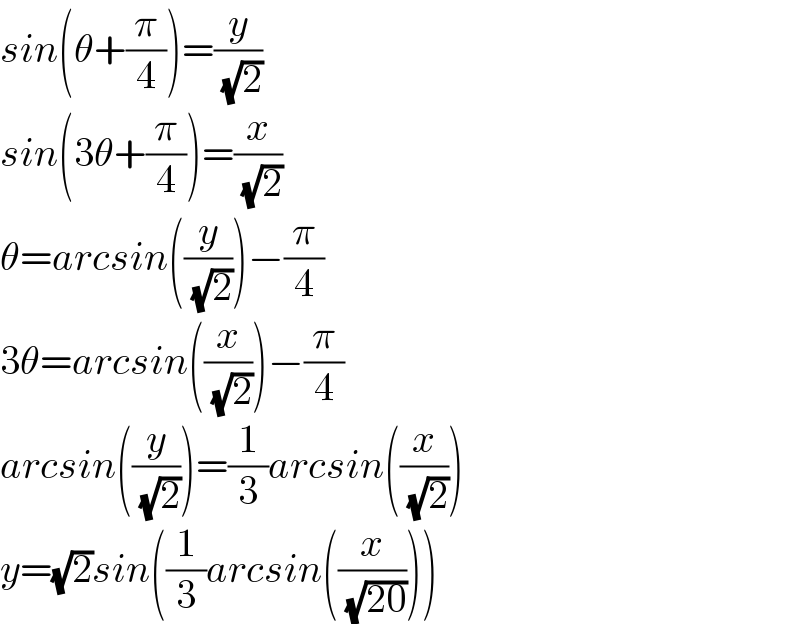
sin(θ+(π/4))=(y/( (√2))) sin(3θ+(π/4))=(x/( (√2))) θ=arcsin((y/( (√2))))−(π/4) 3θ=arcsin((x/( (√2))))−(π/4) arcsin((y/( (√2))))=(1/3)arcsin((x/( (√2)))) y=(√2)sin((1/3)arcsin((x/( (√(20))))))

$${sin}\left(\theta+\frac{\pi}{\mathrm{4}}\right)=\frac{{y}}{\:\sqrt{\mathrm{2}}} \\ $$$${sin}\left(\mathrm{3}\theta+\frac{\pi}{\mathrm{4}}\right)=\frac{{x}}{\:\sqrt{\mathrm{2}}} \\ $$$$\theta={arcsin}\left(\frac{{y}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{3}\theta={arcsin}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\pi}{\mathrm{4}} \\ $$$${arcsin}\left(\frac{{y}}{\:\sqrt{\mathrm{2}}}\right)=\frac{\mathrm{1}}{\mathrm{3}}{arcsin}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$${y}=\sqrt{\mathrm{2}}{sin}\left(\frac{\mathrm{1}}{\mathrm{3}}{arcsin}\left(\frac{{x}}{\:\sqrt{\mathrm{20}}}\right)\right) \\ $$

Commented by mnjuly1970 last updated on 24/Jan/22

$$\:\:\:{mercey}\:{sir}\:… \\ $$

Facebook Tweet Pin

If-sin-3-cos-3-x-sin-cos-y-then-find-a-relationship-between-x-y-indepentent-of-

Leave a Reply Cancel reply