Question Number 128702 by bemath last updated on 09/Jan/21
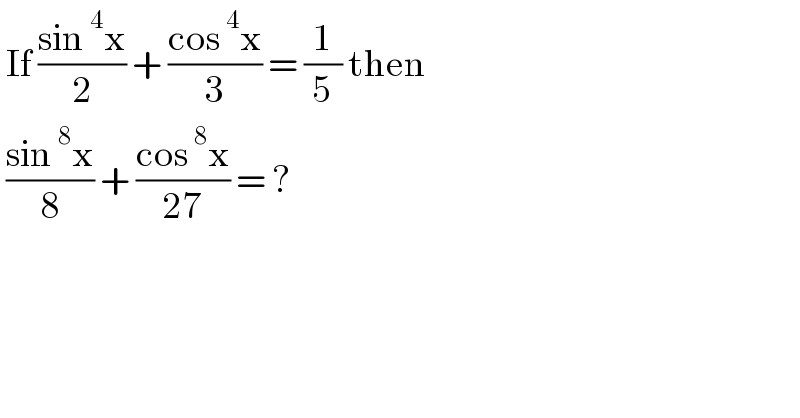
$$\:\mathrm{If}\:\frac{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}}{\mathrm{2}}\:+\:\frac{\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{then}\: \\ $$$$\:\frac{\mathrm{sin}\:^{\mathrm{8}} \mathrm{x}}{\mathrm{8}}\:+\:\frac{\mathrm{cos}\:^{\mathrm{8}} \mathrm{x}}{\mathrm{27}}\:=\:? \\ $$
Answered by liberty last updated on 09/Jan/21
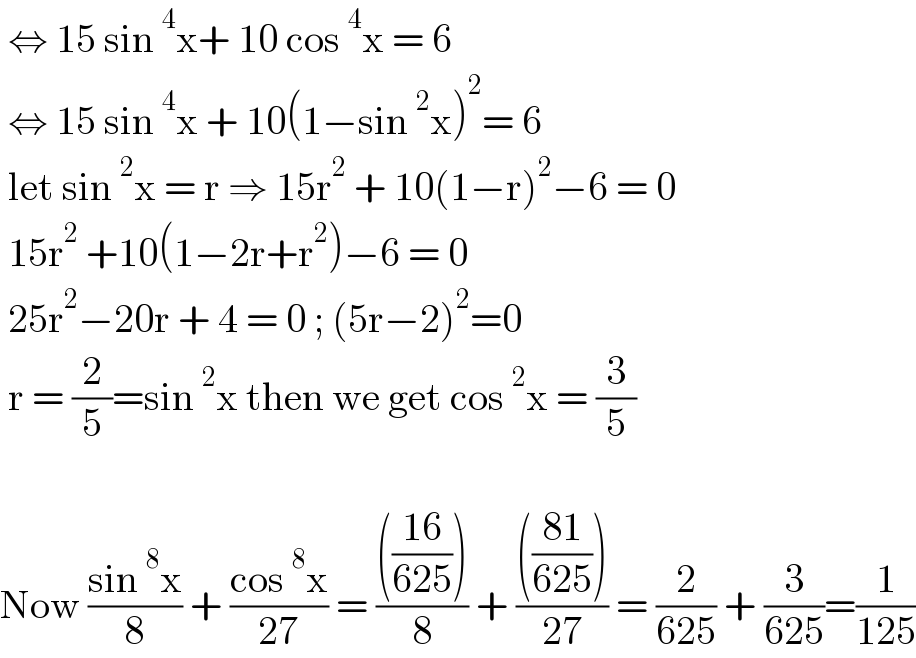
$$\:\Leftrightarrow\:\mathrm{15}\:\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}+\:\mathrm{10}\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}\:=\:\mathrm{6} \\ $$$$\:\Leftrightarrow\:\mathrm{15}\:\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\:+\:\mathrm{10}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} =\:\mathrm{6} \\ $$$$\:\mathrm{let}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:=\:\mathrm{r}\:\Rightarrow\:\mathrm{15r}^{\mathrm{2}} \:+\:\mathrm{10}\left(\mathrm{1}−\mathrm{r}\right)^{\mathrm{2}} −\mathrm{6}\:=\:\mathrm{0} \\ $$$$\:\mathrm{15r}^{\mathrm{2}} \:+\mathrm{10}\left(\mathrm{1}−\mathrm{2r}+\mathrm{r}^{\mathrm{2}} \right)−\mathrm{6}\:=\:\mathrm{0} \\ $$$$\:\mathrm{25r}^{\mathrm{2}} −\mathrm{20r}\:+\:\mathrm{4}\:=\:\mathrm{0}\:;\:\left(\mathrm{5r}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\mathrm{r}\:=\:\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{then}\:\mathrm{we}\:\mathrm{get}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\:=\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{Now}\:\frac{\mathrm{sin}\:^{\mathrm{8}} \mathrm{x}}{\mathrm{8}}\:+\:\frac{\mathrm{cos}\:^{\mathrm{8}} \mathrm{x}}{\mathrm{27}}\:=\:\frac{\left(\frac{\mathrm{16}}{\mathrm{625}}\right)}{\mathrm{8}}\:+\:\frac{\left(\frac{\mathrm{81}}{\mathrm{625}}\right)}{\mathrm{27}}\:=\:\frac{\mathrm{2}}{\mathrm{625}}\:+\:\frac{\mathrm{3}}{\mathrm{625}}=\frac{\mathrm{1}}{\mathrm{125}} \\ $$
