Question Number 116441 by bobhans last updated on 04/Oct/20
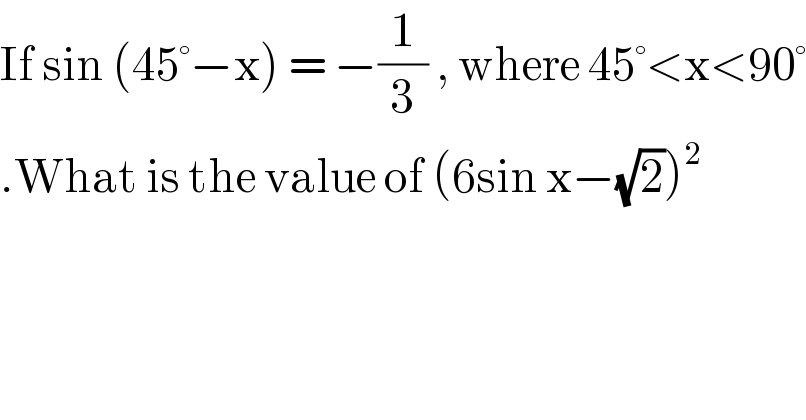
$$\mathrm{If}\:\mathrm{sin}\:\left(\mathrm{45}°−\mathrm{x}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{3}}\:,\:\mathrm{where}\:\mathrm{45}°<\mathrm{x}<\mathrm{90}° \\ $$$$.\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\left(\mathrm{6sin}\:\mathrm{x}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$
Answered by bemath last updated on 04/Oct/20
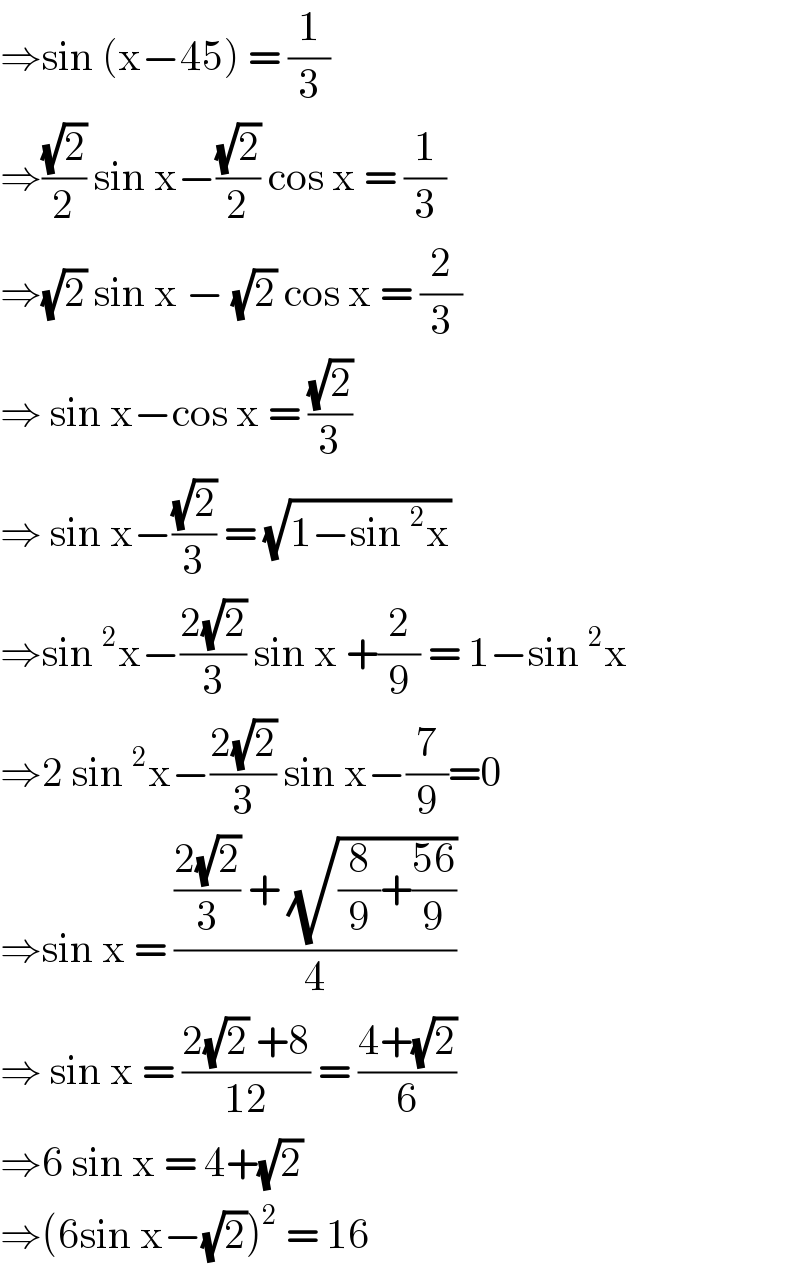
$$\Rightarrow\mathrm{sin}\:\left(\mathrm{x}−\mathrm{45}\right)\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{sin}\:\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{x}\:−\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\:=\:\sqrt{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}} \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x}\:+\frac{\mathrm{2}}{\mathrm{9}}\:=\:\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:\mathrm{sin}\:\mathrm{x}−\frac{\mathrm{7}}{\mathrm{9}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{x}\:=\:\frac{\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:+\:\sqrt{\frac{\mathrm{8}}{\mathrm{9}}+\frac{\mathrm{56}}{\mathrm{9}}}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{x}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{8}}{\mathrm{12}}\:=\:\frac{\mathrm{4}+\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{6}\:\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{4}+\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{6sin}\:\mathrm{x}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:=\:\mathrm{16} \\ $$
Commented by bobhans last updated on 04/Oct/20

$$\mathrm{cooll} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Oct/20
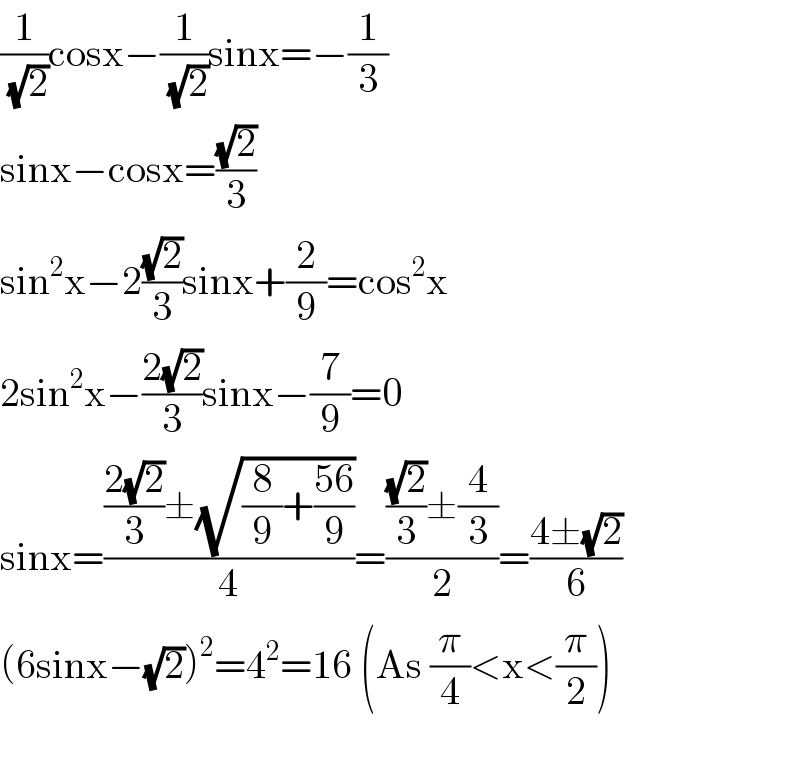
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{cosx}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{sinx}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{sinx}−\mathrm{cosx}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{2}\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{sinx}+\frac{\mathrm{2}}{\mathrm{9}}=\mathrm{cos}^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{2sin}^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{sinx}−\frac{\mathrm{7}}{\mathrm{9}}=\mathrm{0} \\ $$$$\mathrm{sinx}=\frac{\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\pm\sqrt{\frac{\mathrm{8}}{\mathrm{9}}+\frac{\mathrm{56}}{\mathrm{9}}}}{\mathrm{4}}=\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\pm\frac{\mathrm{4}}{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{4}\pm\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$$\left(\mathrm{6sinx}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} =\mathrm{16}\:\left(\mathrm{As}\:\frac{\pi}{\mathrm{4}}<\mathrm{x}<\frac{\pi}{\mathrm{2}}\right) \\ $$$$ \\ $$
