Question Number 95324 by I want to learn more last updated on 24/May/20
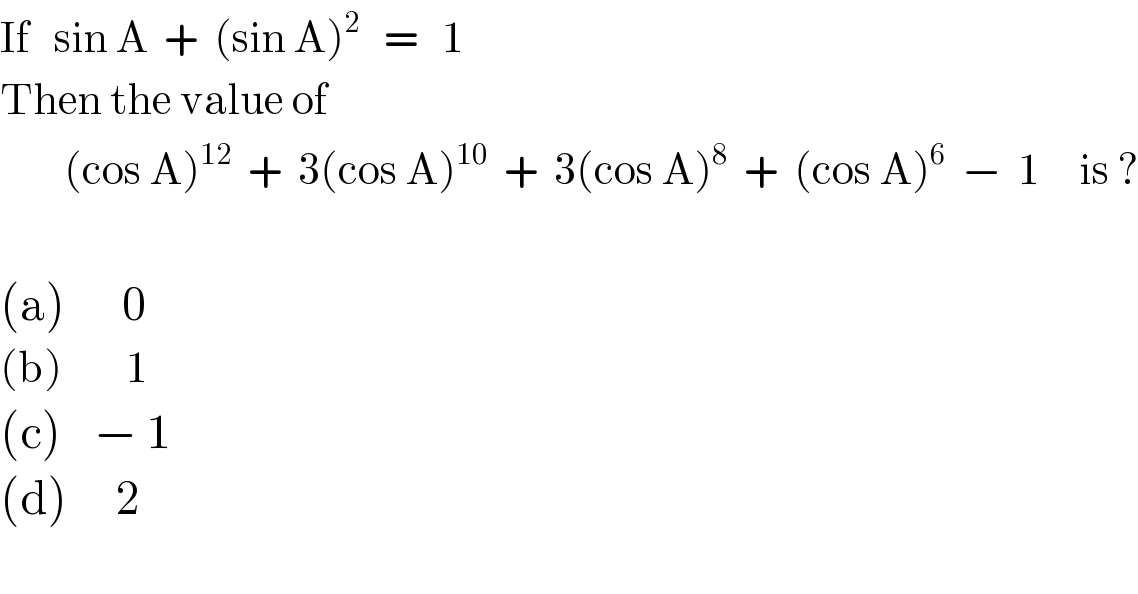
$$\mathrm{If}\:\:\:\mathrm{sin}\:\mathrm{A}\:\:+\:\:\left(\mathrm{sin}\:\mathrm{A}\right)^{\mathrm{2}} \:\:\:=\:\:\:\mathrm{1} \\ $$$$\mathrm{Then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{cos}\:\mathrm{A}\right)^{\mathrm{12}} \:\:+\:\:\mathrm{3}\left(\mathrm{cos}\:\mathrm{A}\right)^{\mathrm{10}} \:\:+\:\:\mathrm{3}\left(\mathrm{cos}\:\mathrm{A}\right)^{\mathrm{8}} \:\:+\:\:\left(\mathrm{cos}\:\mathrm{A}\right)^{\mathrm{6}} \:\:−\:\:\mathrm{1}\:\:\:\:\:\mathrm{is}\:? \\ $$$$ \\ $$$$\left(\mathrm{a}\right)\:\:\:\:\:\:\:\mathrm{0} \\ $$$$\left(\mathrm{b}\right)\:\:\:\:\:\:\:\:\mathrm{1} \\ $$$$\left(\mathrm{c}\right)\:\:\:\:−\:\mathrm{1} \\ $$$$\left(\mathrm{d}\right)\:\:\:\:\:\:\mathrm{2} \\ $$
Commented by bobhans last updated on 24/May/20
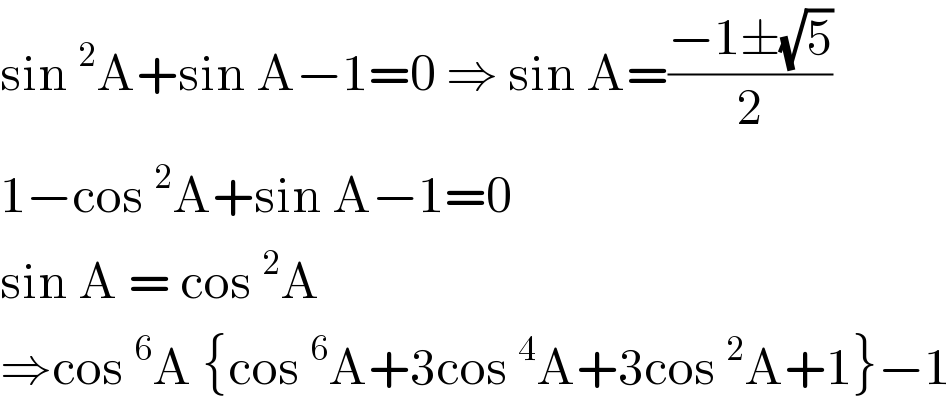
$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}+\mathrm{sin}\:\mathrm{A}−\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{sin}\:\mathrm{A}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{A}+\mathrm{sin}\:\mathrm{A}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}\:\mathrm{A}\:=\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{A} \\ $$$$\Rightarrow\mathrm{cos}\:^{\mathrm{6}} \mathrm{A}\:\left\{\mathrm{cos}\:^{\mathrm{6}} \mathrm{A}+\mathrm{3cos}\:^{\mathrm{4}} \mathrm{A}+\mathrm{3cos}\:^{\mathrm{2}} \mathrm{A}+\mathrm{1}\right\}−\mathrm{1} \\ $$
Commented by bobhans last updated on 24/May/20
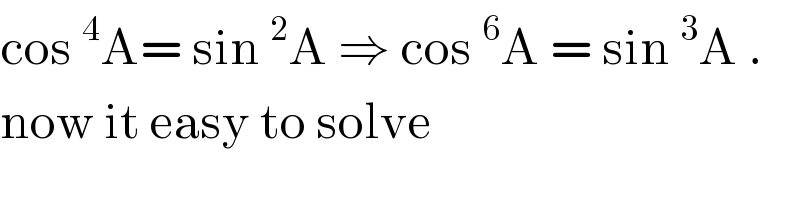
$$\mathrm{cos}\:^{\mathrm{4}} \mathrm{A}=\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}\:\Rightarrow\:\mathrm{cos}\:^{\mathrm{6}} \mathrm{A}\:=\:\mathrm{sin}\:^{\mathrm{3}} \mathrm{A}\:.\: \\ $$$$\mathrm{now}\:\mathrm{it}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve} \\ $$
