Question Number 26778 by tawa tawa last updated on 29/Dec/17
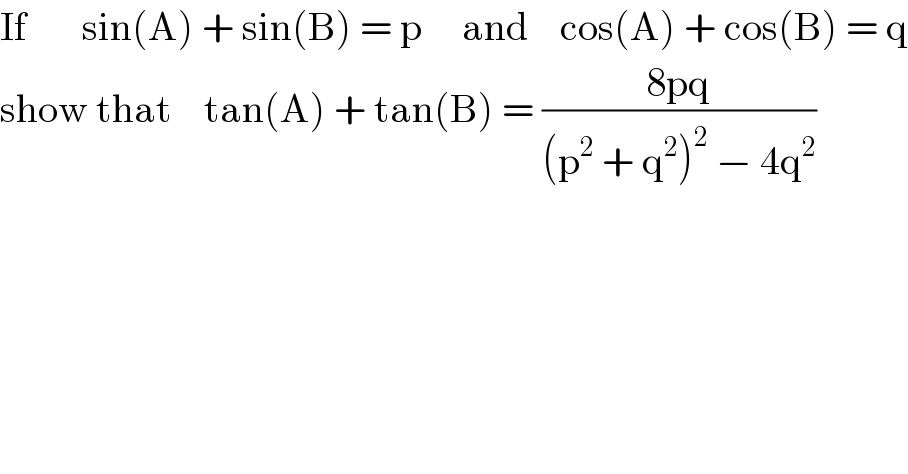
$$\mathrm{If}\:\:\:\:\:\:\:\mathrm{sin}\left(\mathrm{A}\right)\:+\:\mathrm{sin}\left(\mathrm{B}\right)\:=\:\mathrm{p}\:\:\:\:\:\mathrm{and}\:\:\:\:\mathrm{cos}\left(\mathrm{A}\right)\:+\:\mathrm{cos}\left(\mathrm{B}\right)\:=\:\mathrm{q} \\ $$$$\mathrm{show}\:\mathrm{that}\:\:\:\:\mathrm{tan}\left(\mathrm{A}\right)\:+\:\mathrm{tan}\left(\mathrm{B}\right)\:=\:\frac{\mathrm{8pq}}{\left(\mathrm{p}^{\mathrm{2}} \:+\:\mathrm{q}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\:\mathrm{4q}^{\mathrm{2}} } \\ $$
Commented by tawa tawa last updated on 29/Dec/17
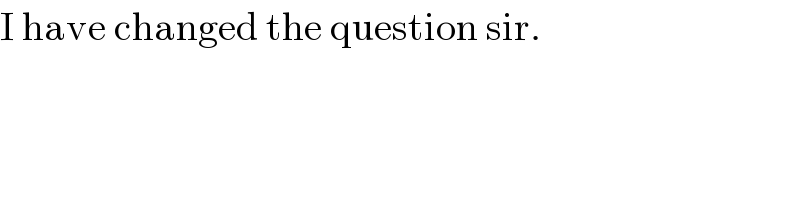
$$\mathrm{I}\:\mathrm{have}\:\mathrm{changed}\:\mathrm{the}\:\mathrm{question}\:\mathrm{sir}. \\ $$
Answered by ajfour last updated on 29/Dec/17
)/((p^2 +1)(p^2 +q^2 )−4p^2 )) .](https://www.tinkutara.com/question/Q26789.png)
$$\mathrm{tan}\:{A}+\mathrm{tan}\:{B}= \\ $$$$\:\:\:\:\:\:\frac{\left[\mathrm{2}−\left({p}−{q}\right)^{\mathrm{2}} \right]\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{\left({p}^{\mathrm{2}} +\mathrm{1}\right)\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−\mathrm{4}{p}^{\mathrm{2}} }\:. \\ $$
Commented by tawa tawa last updated on 29/Dec/17

$$\mathrm{please}\:\mathrm{prove}\:\mathrm{this}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
