Question Number 82767 by jagoll last updated on 24/Feb/20
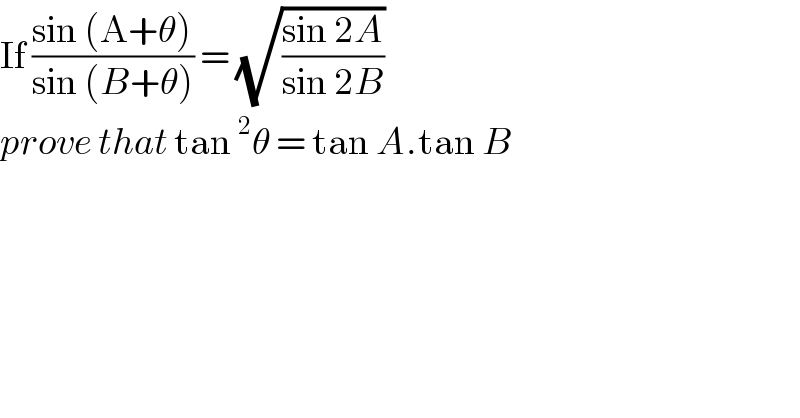
$$\mathrm{If}\:\frac{\mathrm{sin}\:\left(\mathrm{A}+\theta\right)}{\mathrm{sin}\:\left({B}+\theta\right)}\:=\:\sqrt{\frac{\mathrm{sin}\:\mathrm{2}{A}}{\mathrm{sin}\:\mathrm{2}{B}}} \\ $$$${prove}\:{that}\:\mathrm{tan}\:^{\mathrm{2}} \theta\:=\:\mathrm{tan}\:{A}.\mathrm{tan}\:{B} \\ $$
Commented by jagoll last updated on 24/Feb/20

$${thank}\:{you}\:{mr}\:{w}\:{and}\:{john} \\ $$
Answered by mr W last updated on 24/Feb/20

$$\frac{\mathrm{sin}\:{A}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{A}\:\mathrm{sin}\:\theta}{\mathrm{sin}\:{B}\:\mathrm{cos}\:\theta+\mathrm{cos}\:{B}\:\mathrm{sin}\:\theta}=\sqrt{\frac{\mathrm{sin}\:{A}\:\mathrm{cos}\:{A}}{\mathrm{sin}\:{B}\:\mathrm{cos}\:{B}}} \\ $$$$\frac{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:{A}}}{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:{B}}}=\frac{\mathrm{sin}\:{B}}{\mathrm{sin}\:{A}}\sqrt{\frac{\mathrm{sin}\:{A}\:\mathrm{cos}\:{A}}{\:\mathrm{sin}\:{B}\:\mathrm{cos}\:{B}}} \\ $$$$\frac{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:{A}}}{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:{B}}}=\sqrt{\frac{\mathrm{tan}\:{B}}{\:\mathrm{tan}\:{A}}} \\ $$$$\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\mathrm{tan}\:{A}}=\sqrt{\frac{\mathrm{tan}\:{B}}{\:\mathrm{tan}\:{A}}}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{tan}\:{A}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}}}\right)\mathrm{tan}\:\theta=\sqrt{\frac{\mathrm{tan}\:{B}}{\:\mathrm{tan}\:{A}}}−\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{A}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{tan}\:{B}}}\right)\mathrm{tan}\:\theta=\sqrt{\mathrm{tan}\:{B}}−\sqrt{\mathrm{tan}\:{A}} \\ $$$$\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}}}=\mathrm{1} \\ $$$$\mathrm{tan}\:\theta=\sqrt{\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}} \\ $$$$\Rightarrow\mathrm{tan}^{\mathrm{2}} \:\theta=\mathrm{tan}\:{A}\:\mathrm{tan}\:{B} \\ $$
