Question Number 127500 by mr W last updated on 30/Dec/20
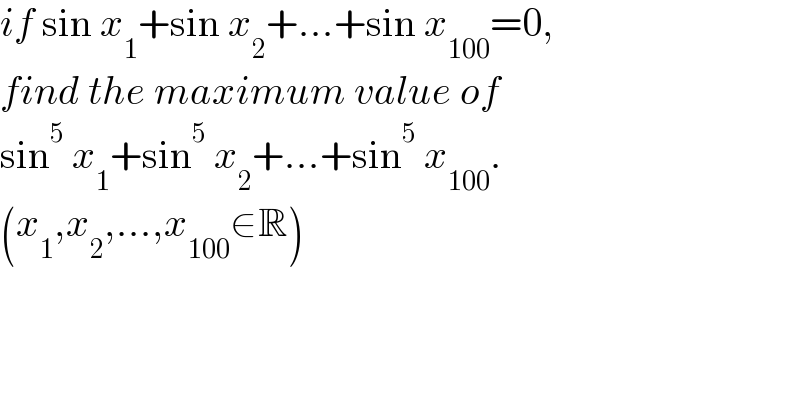
$${if}\:\mathrm{sin}\:{x}_{\mathrm{1}} +\mathrm{sin}\:{x}_{\mathrm{2}} +…+\mathrm{sin}\:{x}_{\mathrm{100}} =\mathrm{0}, \\ $$$${find}\:{the}\:{maximum}\:{value}\:{of} \\ $$$$\mathrm{sin}^{\mathrm{5}} \:{x}_{\mathrm{1}} +\mathrm{sin}^{\mathrm{5}} \:{x}_{\mathrm{2}} +…+\mathrm{sin}^{\mathrm{5}} \:{x}_{\mathrm{100}} . \\ $$$$\left({x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,…,{x}_{\mathrm{100}} \in\mathbb{R}\right) \\ $$
Answered by mr W last updated on 31/Dec/20
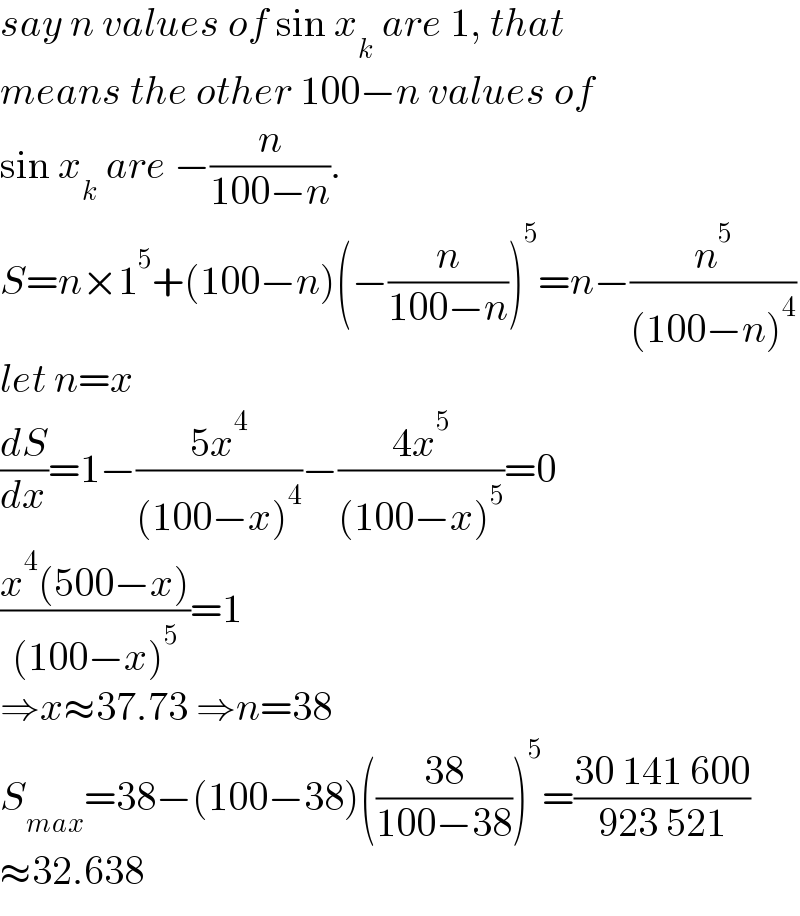
$${say}\:{n}\:{values}\:{of}\:\mathrm{sin}\:{x}_{{k}} \:{are}\:\mathrm{1},\:{that} \\ $$$${means}\:{the}\:{other}\:\mathrm{100}−{n}\:{values}\:{of} \\ $$$$\mathrm{sin}\:{x}_{{k}} \:{are}\:−\frac{{n}}{\mathrm{100}−{n}}. \\ $$$${S}={n}×\mathrm{1}^{\mathrm{5}} +\left(\mathrm{100}−{n}\right)\left(−\frac{{n}}{\mathrm{100}−{n}}\right)^{\mathrm{5}} ={n}−\frac{{n}^{\mathrm{5}} }{\left(\mathrm{100}−{n}\right)^{\mathrm{4}} } \\ $$$${let}\:{n}={x} \\ $$$$\frac{{dS}}{{dx}}=\mathrm{1}−\frac{\mathrm{5}{x}^{\mathrm{4}} }{\left(\mathrm{100}−{x}\right)^{\mathrm{4}} }−\frac{\mathrm{4}{x}^{\mathrm{5}} }{\left(\mathrm{100}−{x}\right)^{\mathrm{5}} }=\mathrm{0} \\ $$$$\frac{{x}^{\mathrm{4}} \left(\mathrm{500}−{x}\right)}{\left(\mathrm{100}−{x}\right)^{\mathrm{5}} }=\mathrm{1} \\ $$$$\Rightarrow{x}\approx\mathrm{37}.\mathrm{73}\:\Rightarrow{n}=\mathrm{38} \\ $$$${S}_{{max}} =\mathrm{38}−\left(\mathrm{100}−\mathrm{38}\right)\left(\frac{\mathrm{38}}{\mathrm{100}−\mathrm{38}}\right)^{\mathrm{5}} =\frac{\mathrm{30}\:\mathrm{141}\:\mathrm{600}}{\mathrm{923}\:\mathrm{521}} \\ $$$$\approx\mathrm{32}.\mathrm{638} \\ $$
