If-sin-x-cos-x-1-3-then-sin-3-x-cos-3-x-

Question Number 127944 by liberty last updated on 03/Jan/21

If \sin x + \cos x = \frac{1}{3} then \sin^{3} x + \cos^{3} x = ?

Answered by mr W last updated on 03/Jan/21

p_{n} = \sin^{n} x + \cos^{n} x

p_{1} = \frac{1}{3} = e_{1}

p_{2} = e_{1}^{2} - 2 e_{2} = \frac{1}{9} - 2 e_{2} = 1 \Rightarrow e_{2} = - \frac{4}{9}

p_{3} = e_{1}^{3} - 3 e_{1} e_{2} = \frac{1}{27} + 3 \times \frac{1}{3} \times \frac{4}{9} = \frac{13}{27}

i . e . \sin^{3} x + \cos^{3} x = \frac{13}{27}

Commented by bramlexs22 last updated on 04/Jan/21

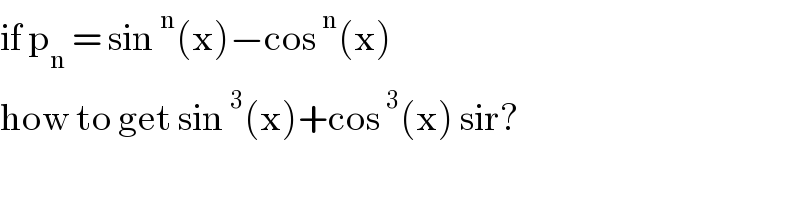
if p_{n} = \sin^{n} (x) - \cos^{n} (x)

how to get \sin^{3} (x) + \cos^{3} (x) sir ?

Commented by mr W last updated on 04/Jan/21

w i t h p_{n} = \sin^{n} (x) - \cos^{n} (x) y o u g e t

u s i n g t h i s m e t h o d c o r e s p o n d i n g l y

\sin^{3} (x) - \cos^{3} (x) .

Answered by bramlexs22 last updated on 03/Jan/21

Commented by mr W last updated on 03/Jan/21

i n q u e s t i o n : \sin x + \cos x = \frac{1}{3}, n o t

\sin x - \cos x = \frac{1}{3} .

Commented by bramlexs22 last updated on 03/Jan/21

�� misread...

Commented by liberty last updated on 03/Jan/21

hahahaha

Answered by mathmax by abdo last updated on 03/Jan/21

\sin^{3} x + \cos^{3} x = (sinx + cosx) (\sin^{2} x - sinx cosx + \cos^{2} x)

= \frac{1}{3} (1 - sinx cosx) we have {(cosx + sinx)}^{2} = \frac{1}{9} \Rightarrow

1 + 2 cosx sinx = \frac{1}{9} \Rightarrow 2 cosx sinx = \frac{1}{9} - 1 = - \frac{8}{9} \Rightarrow cosx sinx = - \frac{4}{9}

\Rightarrow \cos^{3} x + \sin^{3} x = \frac{1}{3} (1 + \frac{4}{9}) = \frac{1}{3} \times \frac{13}{9} = \frac{13}{27}