Question Number 20886 by tammi last updated on 06/Sep/17

$${if}\:\mathrm{sin}\:{x}={m}\mathrm{sin}\:{y} \\ $$$${so}\:{proof}\:{that} \\ $$$$\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{y}\right)=\frac{{m}−\mathrm{1}}{{m}+\mathrm{1}}\mathrm{tan}\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}\right) \\ $$
Answered by ajfour last updated on 06/Sep/17
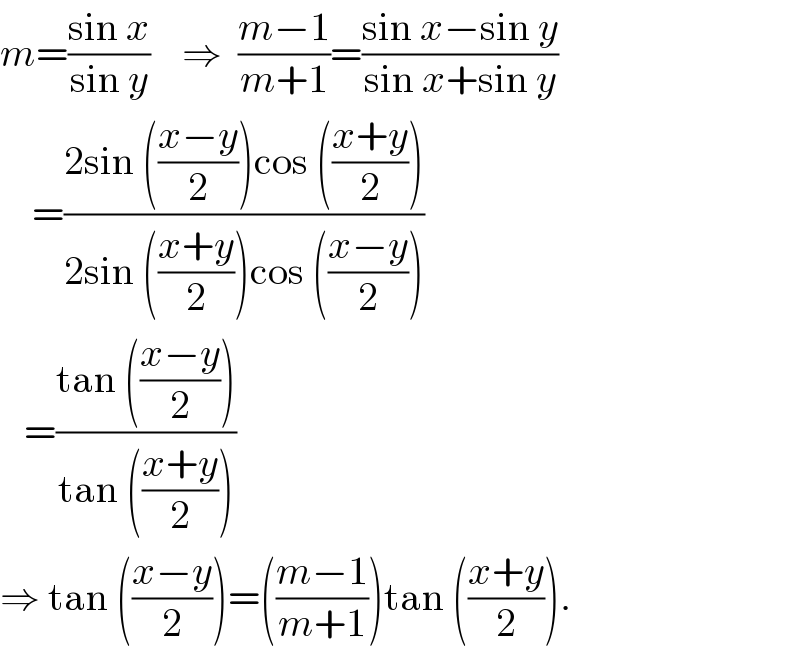
$${m}=\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{y}}\:\:\:\:\Rightarrow\:\:\frac{{m}−\mathrm{1}}{{m}+\mathrm{1}}=\frac{\mathrm{sin}\:{x}−\mathrm{sin}\:{y}}{\mathrm{sin}\:{x}+\mathrm{sin}\:{y}} \\ $$$$\:\:\:\:=\frac{\mathrm{2sin}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)}{\mathrm{2sin}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\mathrm{tan}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)}{\mathrm{tan}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\:\mathrm{tan}\:\left(\frac{{x}−{y}}{\mathrm{2}}\right)=\left(\frac{{m}−\mathrm{1}}{{m}+\mathrm{1}}\right)\mathrm{tan}\:\left(\frac{{x}+{y}}{\mathrm{2}}\right). \\ $$
