Menu Close

If-sinA-cos2A-1-2-and-cosA-sin2A-1-3-then-find-the-value-of-sin3A-

Tinku Tara 0 Comments
Pin




Question Number 51069 by rahul 19 last updated on 23/Dec/18
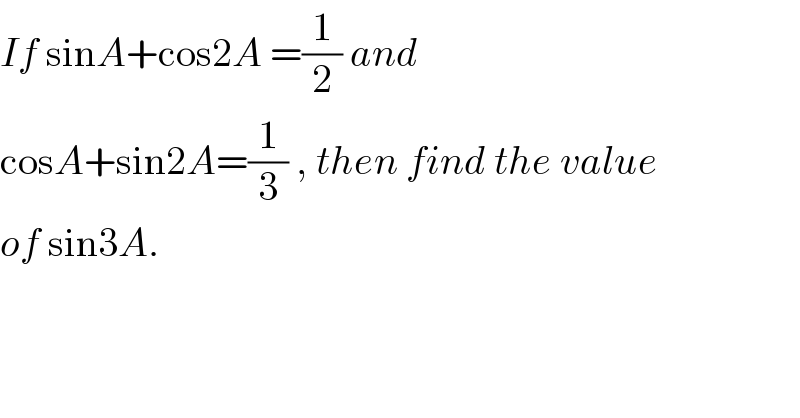
If sinA+cos2A =(1/2) and cosA+sin2A=(1/3) , then find the value of sin3A.
$${If}\:\mathrm{sin}{A}+\mathrm{cos2}{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\:{and} \\ $$$$\mathrm{cos}{A}+\mathrm{sin2}{A}=\frac{\mathrm{1}}{\mathrm{3}}\:,\:{then}\:{find}\:{the}\:{value} \\ $$$${of}\:\mathrm{sin3}{A}. \\ $$
Answered by peter frank last updated on 23/Dec/18
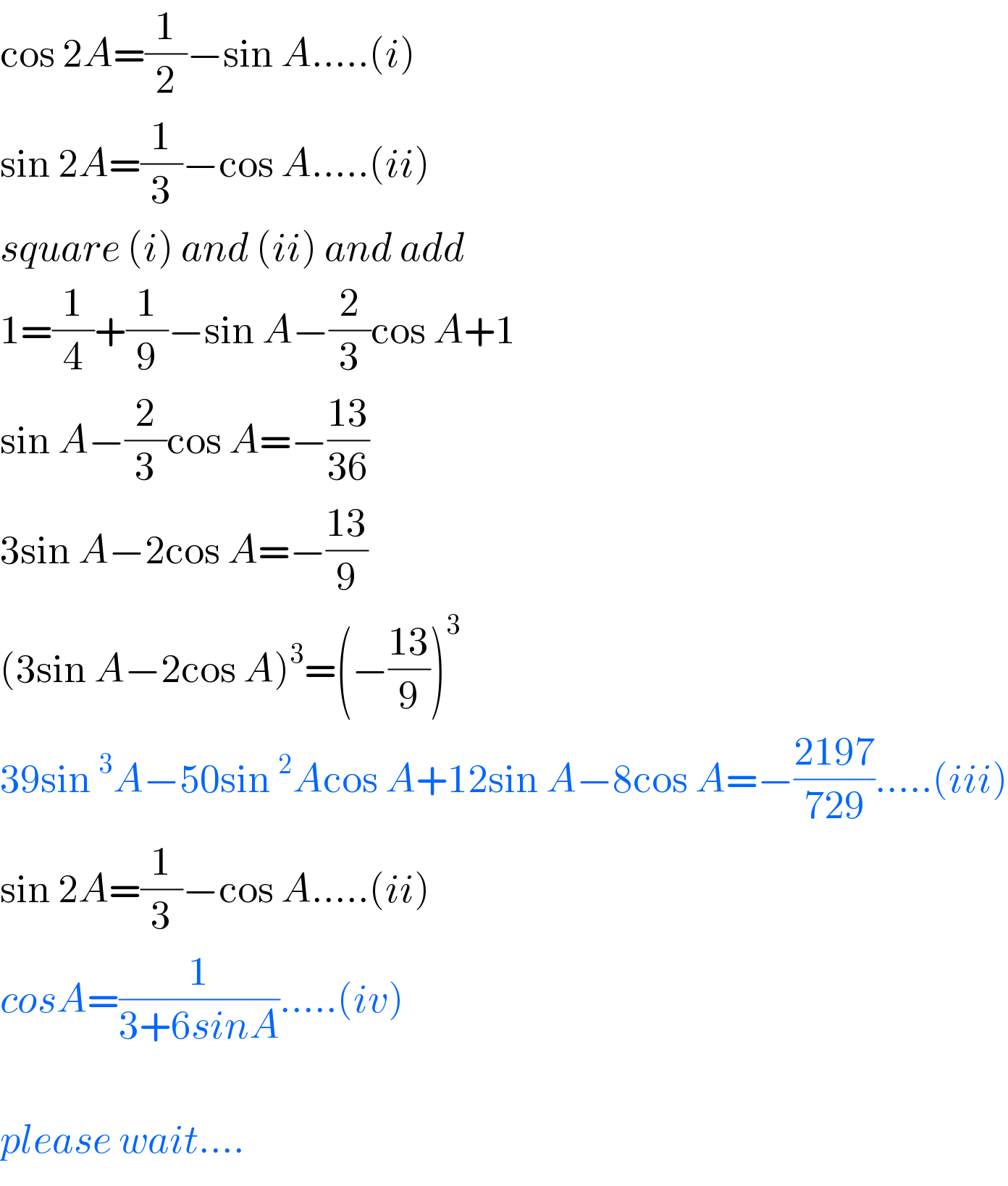
cos 2A=(1/2)−sin A.....(i) sin 2A=(1/3)−cos A.....(ii) square (i) and (ii) and add 1=(1/4)+(1/9)−sin A−(2/3)cos A+1 sin A−(2/3)cos A=−((13)/(36)) 3sin A−2cos A=−((13)/9) (3sin A−2cos A)^3 =(−((13)/9))^3 39sin^3 A−50sin^2 Acos A+12sin A−8cos A=−((2197)/(729)).....(iii) sin 2A=(1/3)−cos A.....(ii) cosA=(1/(3+6sinA)).....(iv) please wait....
$$\mathrm{cos}\:\mathrm{2}{A}=\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{sin}\:{A}…..\left({i}\right) \\ $$$$\mathrm{sin}\:\mathrm{2}{A}=\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{cos}\:{A}…..\left({ii}\right) \\ $$$${square}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{and}\:{add} \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{9}}−\mathrm{sin}\:{A}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:{A}+\mathrm{1} \\ $$$$\mathrm{sin}\:{A}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{cos}\:{A}=−\frac{\mathrm{13}}{\mathrm{36}} \\ $$$$\mathrm{3sin}\:{A}−\mathrm{2cos}\:{A}=−\frac{\mathrm{13}}{\mathrm{9}} \\ $$$$\left(\mathrm{3sin}\:{A}−\mathrm{2cos}\:{A}\right)^{\mathrm{3}} =\left(−\frac{\mathrm{13}}{\mathrm{9}}\right)^{\mathrm{3}} \\ $$$$\mathrm{39sin}\:^{\mathrm{3}} {A}−\mathrm{50sin}\:^{\mathrm{2}} {A}\mathrm{cos}\:{A}+\mathrm{12sin}\:{A}−\mathrm{8cos}\:{A}=−\frac{\mathrm{2197}}{\mathrm{729}}…..\left({iii}\right) \\ $$$$\mathrm{sin}\:\mathrm{2}{A}=\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{cos}\:{A}…..\left({ii}\right) \\ $$$${cosA}=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{6}{sinA}}…..\left({iv}\right) \\ $$$$ \\ $$$${please}\:{wait}…. \\ $$
Answered by MJS last updated on 23/Dec/18
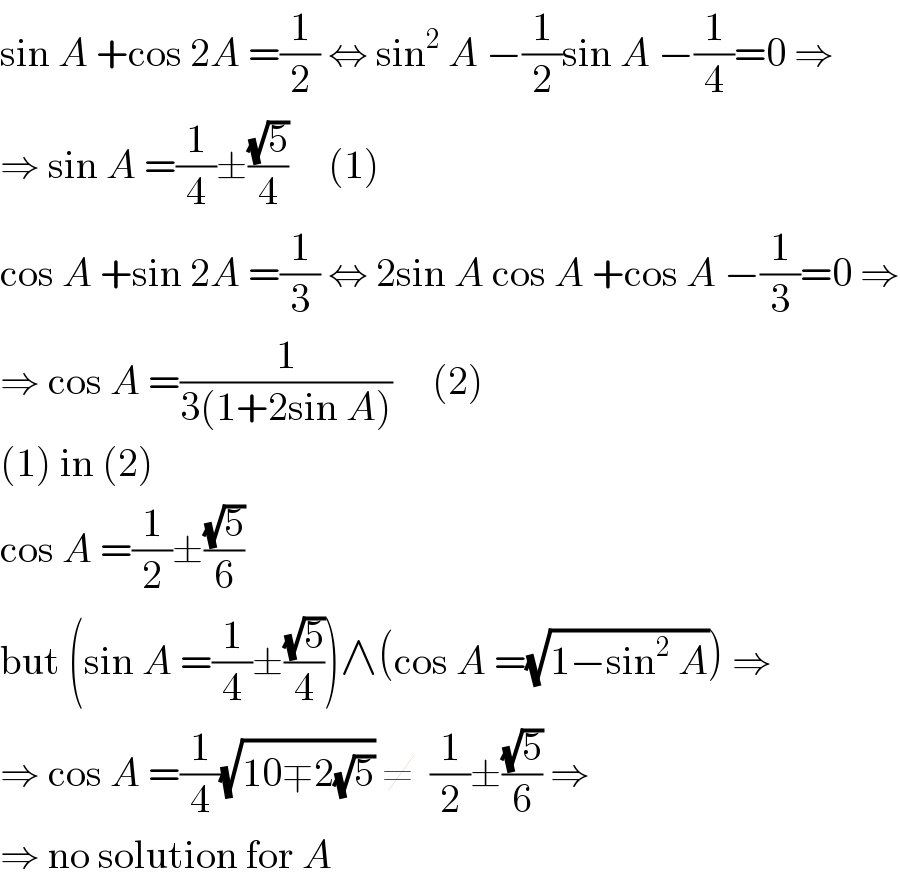
sin A +cos 2A =(1/2) ⇔ sin^2 A −(1/2)sin A −(1/4)=0 ⇒ ⇒ sin A =(1/4)±((√5)/4) (1) cos A +sin 2A =(1/3) ⇔ 2sin A cos A +cos A −(1/3)=0 ⇒ ⇒ cos A =(1/(3(1+2sin A))) (2) (1) in (2) cos A =(1/2)±((√5)/6) but (sin A =(1/4)±((√5)/4))∧(cos A =(√(1−sin^2 A))) ⇒ ⇒ cos A =(1/4)(√(10∓2(√5))) ≠ (1/2)±((√5)/6) ⇒ ⇒ no solution for A
$$\mathrm{sin}\:{A}\:+\mathrm{cos}\:\mathrm{2}{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Leftrightarrow\:\mathrm{sin}^{\mathrm{2}} \:{A}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{A}\:−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{sin}\:{A}\:=\frac{\mathrm{1}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{cos}\:{A}\:+\mathrm{sin}\:\mathrm{2}{A}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Leftrightarrow\:\mathrm{2sin}\:{A}\:\mathrm{cos}\:{A}\:+\mathrm{cos}\:{A}\:−\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{cos}\:{A}\:=\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+\mathrm{2sin}\:{A}\right)}\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)\:\mathrm{in}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{cos}\:{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{6}} \\ $$$$\mathrm{but}\:\left(\mathrm{sin}\:{A}\:=\frac{\mathrm{1}}{\mathrm{4}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{4}}\right)\wedge\left(\mathrm{cos}\:{A}\:=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{A}}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{cos}\:{A}\:=\frac{\mathrm{1}}{\mathrm{4}}\sqrt{\mathrm{10}\mp\mathrm{2}\sqrt{\mathrm{5}}}\:\neq\:\:\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}\:\Rightarrow \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{A} \\ $$
Commented by rahul 19 last updated on 24/Dec/18
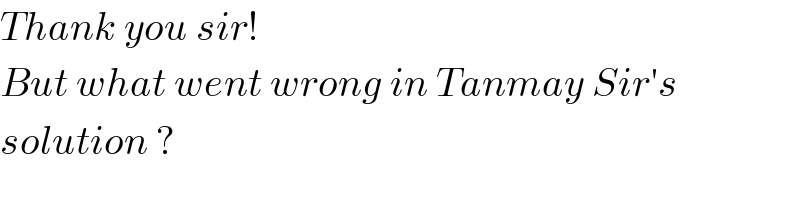
Thank you sir! But what went wrong in Tanmay Sir′s solution ?
$${Thank}\:{you}\:{sir}! \\ $$$${But}\:{what}\:{went}\:{wrong}\:{in}\:{Tanmay}\:{Sir}'{s} \\ $$$${solution}\:? \\ $$
Commented by mr W last updated on 24/Dec/18
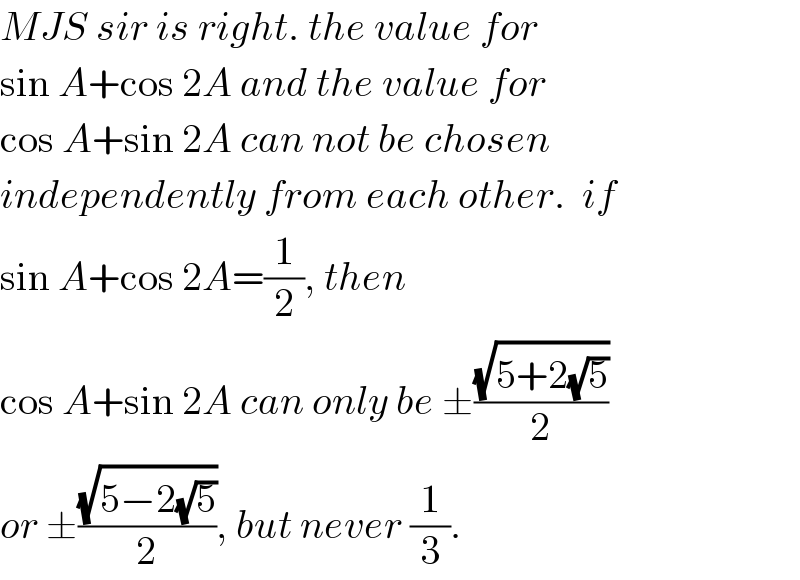
MJS sir is right. the value for sin A+cos 2A and the value for cos A+sin 2A can not be chosen independently from each other. if sin A+cos 2A=(1/2), then cos A+sin 2A can only be ±((√(5+2(√5)))/2) or ±((√(5−2(√5)))/2), but never (1/3).
$${MJS}\:{sir}\:{is}\:{right}.\:{the}\:{value}\:{for} \\ $$$$\mathrm{sin}\:{A}+\mathrm{cos}\:\mathrm{2}{A}\:{and}\:{the}\:{value}\:{for} \\ $$$$\mathrm{cos}\:{A}+\mathrm{sin}\:\mathrm{2}{A}\:{can}\:{not}\:{be}\:{chosen} \\ $$$${independently}\:{from}\:{each}\:{other}.\:\:{if} \\ $$$$\mathrm{sin}\:{A}+\mathrm{cos}\:\mathrm{2}{A}=\frac{\mathrm{1}}{\mathrm{2}},\:{then} \\ $$$$\mathrm{cos}\:{A}+\mathrm{sin}\:\mathrm{2}{A}\:{can}\:{only}\:{be}\:\pm\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$${or}\:\pm\frac{\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}},\:{but}\:{never}\:\frac{\mathrm{1}}{\mathrm{3}}. \\ $$
Commented by MJS last updated on 24/Dec/18
you can “solve” in many ways sin^2 A −(1/2)sin A −(1/4)=0 2sin A cos A +cos A −(1/3)=0 write s for sin A and c for cos A s^2 −(1/2)s−(1/4)=0 (1) 2sc+c−(1/3)=0 (2) we can solve this system for s and c. but s and c aren′t independent. we have a third equation s^2 +c^2 =1 (3) ⇒ no solution
$$\mathrm{you}\:\mathrm{can}\:“\mathrm{solve}''\:\mathrm{in}\:\mathrm{many}\:\mathrm{ways} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{A}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:{A}\:−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{2sin}\:{A}\:\mathrm{cos}\:{A}\:+\mathrm{cos}\:{A}\:−\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0} \\ $$$$\mathrm{write}\:{s}\:\mathrm{for}\:\mathrm{sin}\:{A}\:\mathrm{and}\:{c}\:\mathrm{for}\:\mathrm{cos}\:{A} \\ $$$${s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}{s}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{2}{sc}+{c}−\frac{\mathrm{1}}{\mathrm{3}}=\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{system}\:\mathrm{for}\:{s}\:\mathrm{and}\:{c}.\:\mathrm{but}\:{s}\:\mathrm{and} \\ $$$${c}\:\mathrm{aren}'\mathrm{t}\:\mathrm{independent}.\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:\mathrm{third}\:\mathrm{equation} \\ $$$${s}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{1}\:\left(\mathrm{3}\right) \\ $$$$\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$
Commented by rahul 19 last updated on 24/Dec/18
Thank you both sirs! Understood now.
$${Thank}\:{you}\:{both}\:{sirs}! \\ $$$${Understood}\:{now}. \\ $$
Answered by mr W last updated on 24/Dec/18
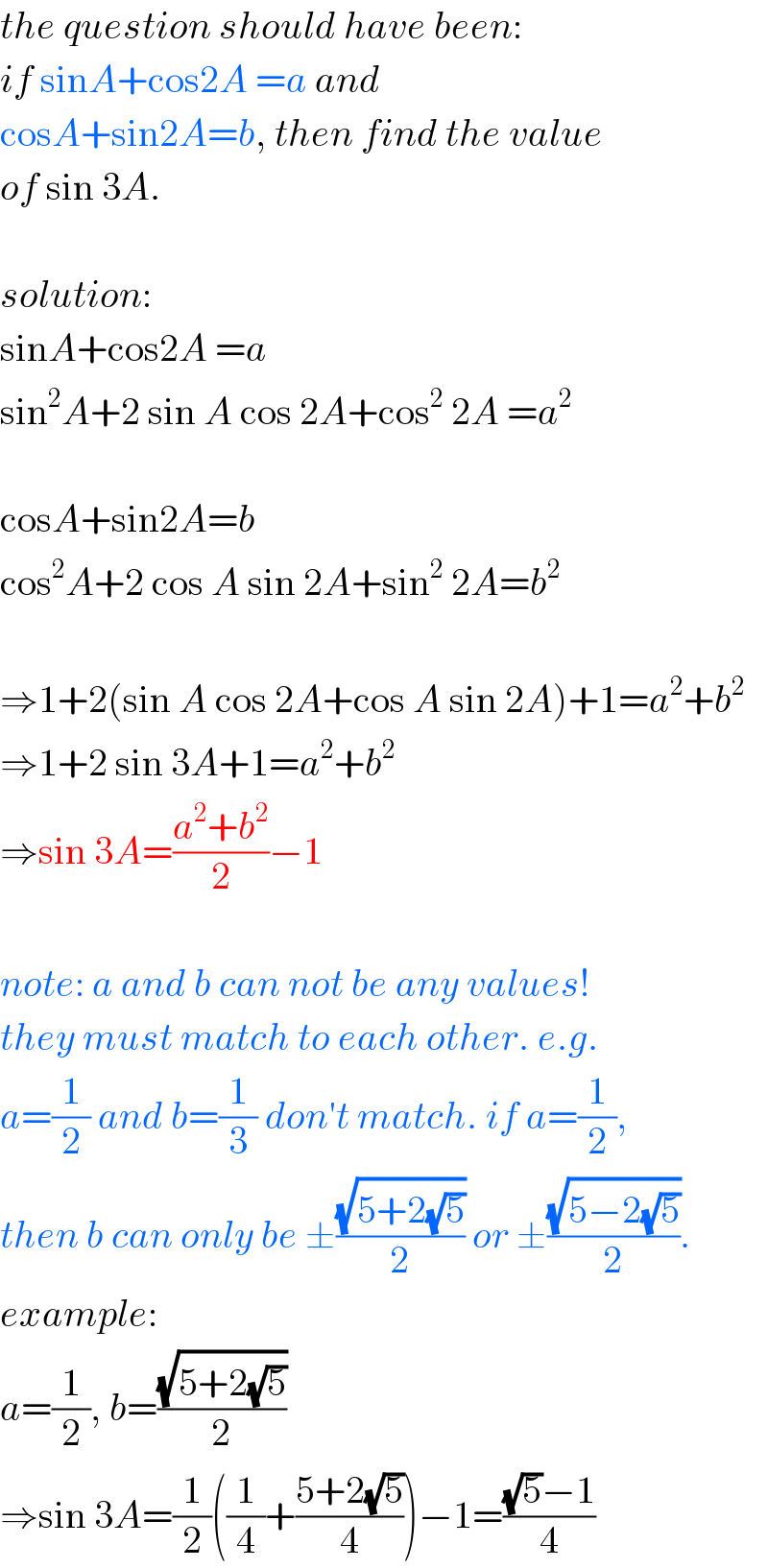
the question should have been: if sinA+cos2A =a and cosA+sin2A=b, then find the value of sin 3A. solution: sinA+cos2A =a sin^2 A+2 sin A cos 2A+cos^2 2A =a^2 cosA+sin2A=b cos^2 A+2 cos A sin 2A+sin^2 2A=b^2 ⇒1+2(sin A cos 2A+cos A sin 2A)+1=a^2 +b^2 ⇒1+2 sin 3A+1=a^2 +b^2 ⇒sin 3A=((a^2 +b^2 )/2)−1 note: a and b can not be any values! they must match to each other. e.g. a=(1/2) and b=(1/3) don′t match. if a=(1/2), then b can only be ±((√(5+2(√5)))/2) or ±((√(5−2(√5)))/2). example: a=(1/2), b=((√(5+2(√5)))/2) ⇒sin 3A=(1/2)((1/4)+((5+2(√5))/4))−1=(((√5)−1)/4)
$${the}\:{question}\:{should}\:{have}\:{been}: \\ $$$${if}\:\mathrm{sin}{A}+\mathrm{cos2}{A}\:={a}\:{and} \\ $$$$\mathrm{cos}{A}+\mathrm{sin2}{A}={b},\:{then}\:{find}\:{the}\:{value} \\ $$$${of}\:\mathrm{sin}\:\mathrm{3}{A}. \\ $$$$ \\ $$$${solution}: \\ $$$$\mathrm{sin}{A}+\mathrm{cos2}{A}\:={a} \\ $$$$\mathrm{sin}^{\mathrm{2}} {A}+\mathrm{2}\:\mathrm{sin}\:{A}\:\mathrm{cos}\:\mathrm{2}{A}+\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}{A}\:={a}^{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{cos}{A}+\mathrm{sin2}{A}={b} \\ $$$$\mathrm{cos}^{\mathrm{2}} {A}+\mathrm{2}\:\mathrm{cos}\:{A}\:\mathrm{sin}\:\mathrm{2}{A}+\mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{A}={b}^{\mathrm{2}} \\ $$$$ \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}\left(\mathrm{sin}\:{A}\:\mathrm{cos}\:\mathrm{2}{A}+\mathrm{cos}\:{A}\:\mathrm{sin}\:\mathrm{2}{A}\right)+\mathrm{1}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}\:\mathrm{sin}\:\mathrm{3}{A}+\mathrm{1}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{3}{A}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1} \\ $$$$ \\ $$$${note}:\:{a}\:{and}\:{b}\:{can}\:{not}\:{be}\:{any}\:{values}! \\ $$$${they}\:{must}\:{match}\:{to}\:{each}\:{other}.\:{e}.{g}. \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{b}=\frac{\mathrm{1}}{\mathrm{3}}\:{don}'{t}\:{match}.\:{if}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}, \\ $$$${then}\:{b}\:{can}\:{only}\:{be}\:\pm\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}\:{or}\:\pm\frac{\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}. \\ $$$${example}: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2}},\:{b}=\frac{\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\mathrm{3}{A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)−\mathrm{1}=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$
Commented by rahul 19 last updated on 24/Dec/18
Thank you Sir!
$${Thank}\:{you}\:{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *