Question Number 81007 by M±th+et£s last updated on 08/Feb/20
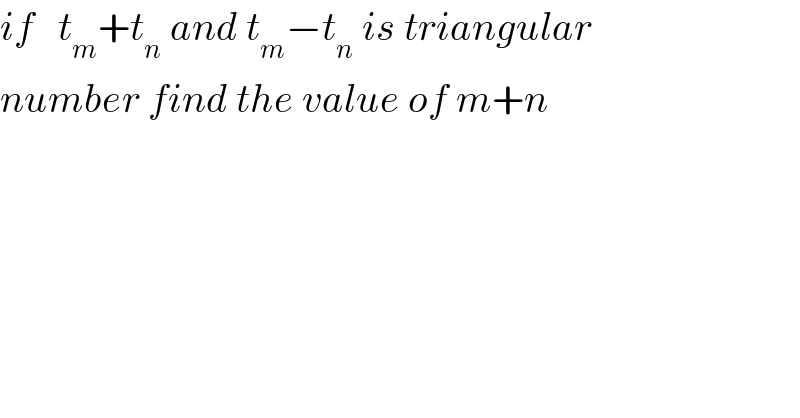
$${if}\:\:\:{t}_{{m}} +{t}_{{n}} \:{and}\:{t}_{{m}} −{t}_{{n}} \:{is}\:{triangular} \\ $$$${number}\:{find}\:{the}\:{value}\:{of}\:{m}+{n} \\ $$
Commented by MJS last updated on 08/Feb/20
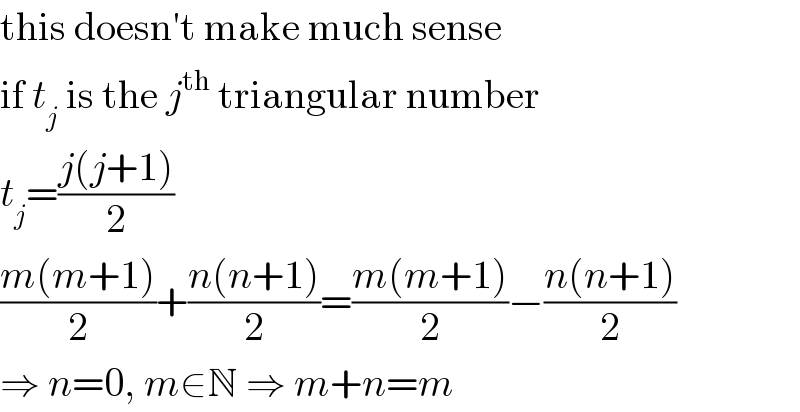
$$\mathrm{this}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{make}\:\mathrm{much}\:\mathrm{sense} \\ $$$$\mathrm{if}\:{t}_{{j}} \:\mathrm{is}\:\mathrm{the}\:{j}^{\mathrm{th}} \:\mathrm{triangular}\:\mathrm{number} \\ $$$${t}_{{j}} =\frac{{j}\left({j}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}}+\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\frac{{m}\left({m}+\mathrm{1}\right)}{\mathrm{2}}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\:{n}=\mathrm{0},\:{m}\in\mathbb{N}\:\Rightarrow\:{m}+{n}={m} \\ $$
