Question Number 94344 by i jagooll last updated on 18/May/20
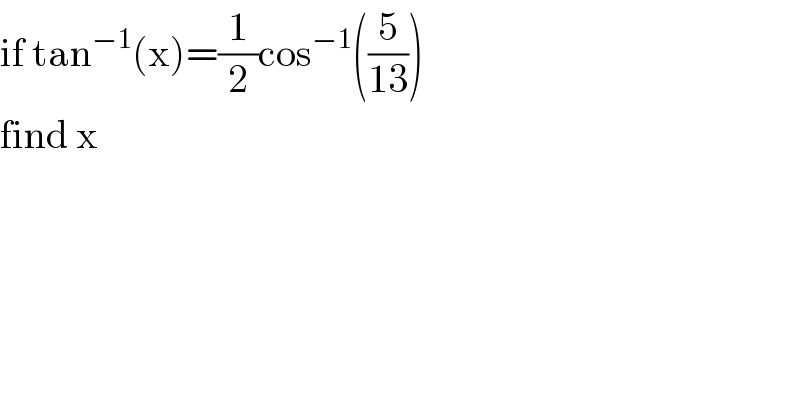
$$\mathrm{if}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{13}}\right) \\ $$$$\mathrm{find}\:\mathrm{x}\: \\ $$
Answered by john santu last updated on 18/May/20

$$\mathrm{let}\:\theta\:=\:\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{13}}\right)\:\Rightarrow\:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{5}}{\mathrm{13}} \\ $$$$\Rightarrow\mathrm{tan}^{−\mathrm{1}} \left({x}\right)=\frac{\theta}{\mathrm{2}}\:\Rightarrow{x}\:=\:\mathrm{tan}\:\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$$\mathrm{remember}\:\mathrm{tan}\:\theta=\:\frac{\mathrm{2tan}\:\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\left(\frac{\theta}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{12}}{\mathrm{5}}\:=\:\frac{\mathrm{2}{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{6}−\mathrm{6}{x}^{\mathrm{2}} =\:\mathrm{5}{x} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{6}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{3}{x}−\mathrm{2}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)\:=\:\mathrm{0}\:\Rightarrow\begin{cases}{{x}=\frac{\mathrm{2}}{\mathrm{3}}}\\{{x}=−\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$$$ \\ $$
Commented by i jagooll last updated on 18/May/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
