Menu Close

if-tan-2-A-tan-2-B-3-0-show-that-cos-2-B-2cos-2-A-0-

Tinku Tara 0 Comments
Pin




Question Number 41389 by mondodotto@gmail.com last updated on 06/Aug/18
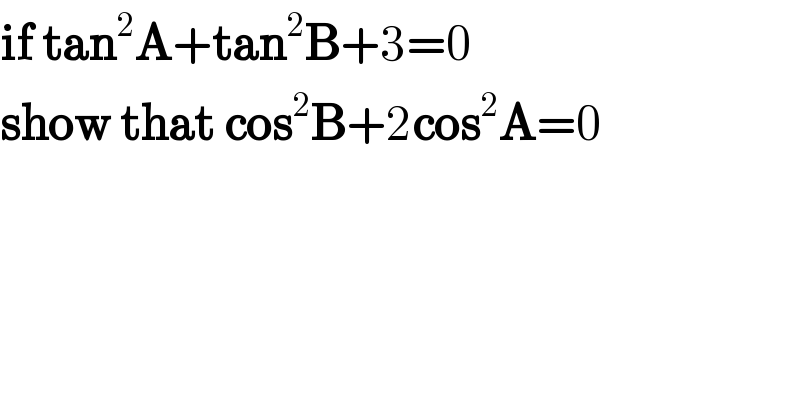
if tan^2 A+tan^2 B+3=0 show that cos^2 B+2cos^2 A=0
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{A}}+\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{B}}+\mathrm{3}=\mathrm{0} \\ $$$$\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{B}}+\mathrm{2}\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \boldsymbol{\mathrm{A}}=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Aug/18
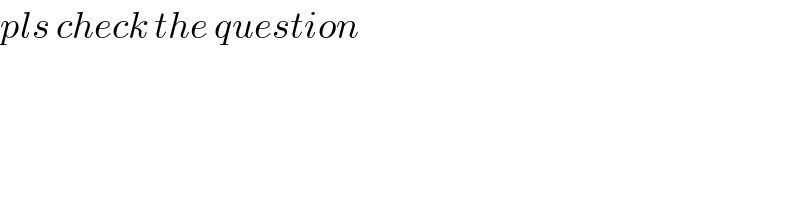
pls check the question
$${pls}\:{check}\:{the}\:{question} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18
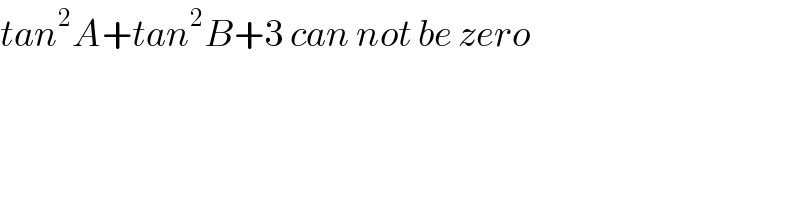
tan^2 A+tan^2 B+3 can not be zero
$${tan}^{\mathrm{2}} {A}+{tan}^{\mathrm{2}} {B}+\mathrm{3}\:{can}\:{not}\:{be}\:{zero} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18
sec^2 A+sec^2 B+1=0 sec^2 B=−1−sec^2 A (1/(cos^2 B))=−(1+(1/(cos^2 A))) (1/(cos^2 B))=−(((1+cos^2 A)/(cos^2 A))) cos^2 B=−(((cos^2 A)/(1+cos^2 A))) so cos^2 B+2cos^2 A =−(((cos^2 A)/(1+cos^2 A)))+2cos^2 A =cos^2 A(2−(1/(1+cos^2 A))) =cos^2 A(((2+2cos^2 A−1)/(1+cos^2 A))) =cos^2 A(((1+2cos^2 A)/(1+cos^2 A))) pls check the question...
$${sec}^{\mathrm{2}} {A}+{sec}^{\mathrm{2}} {B}+\mathrm{1}=\mathrm{0} \\ $$$${sec}^{\mathrm{2}} {B}=−\mathrm{1}−{sec}^{\mathrm{2}} {A} \\ $$$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {B}}=−\left(\mathrm{1}+\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {A}}\right) \\ $$$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {B}}=−\left(\frac{\mathrm{1}+{cos}^{\mathrm{2}} {A}}{{cos}^{\mathrm{2}} {A}}\right) \\ $$$${cos}^{\mathrm{2}} {B}=−\left(\frac{{cos}^{\mathrm{2}} {A}}{\mathrm{1}+{cos}^{\mathrm{2}} {A}}\right) \\ $$$${so}\: \\ $$$${cos}^{\mathrm{2}} {B}+\mathrm{2}{cos}^{\mathrm{2}} {A} \\ $$$$=−\left(\frac{{cos}^{\mathrm{2}} {A}}{\mathrm{1}+{cos}^{\mathrm{2}} {A}}\right)+\mathrm{2}{cos}^{\mathrm{2}} {A} \\ $$$$={cos}^{\mathrm{2}} {A}\left(\mathrm{2}−\frac{\mathrm{1}}{\mathrm{1}+{cos}^{\mathrm{2}} {A}}\right) \\ $$$$={cos}^{\mathrm{2}} {A}\left(\frac{\mathrm{2}+\mathrm{2}{cos}^{\mathrm{2}} {A}−\mathrm{1}}{\mathrm{1}+{cos}^{\mathrm{2}} {A}}\right) \\ $$$$={cos}^{\mathrm{2}} {A}\left(\frac{\mathrm{1}+\mathrm{2}{cos}^{\mathrm{2}} {A}}{\mathrm{1}+{cos}^{\mathrm{2}} {A}}\right) \\ $$$$\boldsymbol{{pls}}\:\boldsymbol{{check}}\:\boldsymbol{{the}}\:\boldsymbol{{question}}… \\ $$$$ \\ $$
Commented by mondodotto@gmail.com last updated on 07/Aug/18
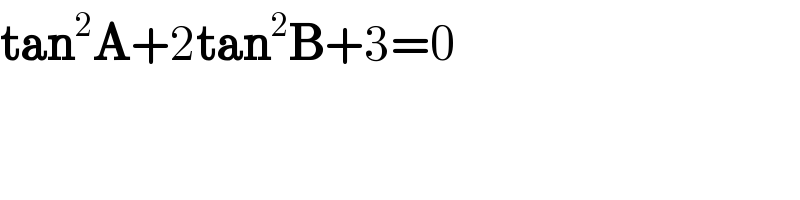
tan^2 A+2tan^2 B+3=0
$$\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{A}}+\mathrm{2}\boldsymbol{\mathrm{tan}}^{\mathrm{2}} \boldsymbol{\mathrm{B}}+\mathrm{3}=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18
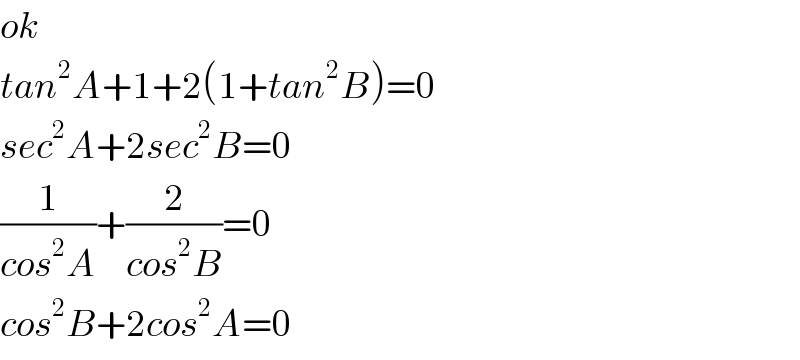
ok tan^2 A+1+2(1+tan^2 B)=0 sec^2 A+2sec^2 B=0 (1/(cos^2 A))+(2/(cos^2 B))=0 cos^2 B+2cos^2 A=0
$${ok} \\ $$$${tan}^{\mathrm{2}} {A}+\mathrm{1}+\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {B}\right)=\mathrm{0} \\ $$$${sec}^{\mathrm{2}} {A}+\mathrm{2}{sec}^{\mathrm{2}} {B}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {A}}+\frac{\mathrm{2}}{{cos}^{\mathrm{2}} {B}}=\mathrm{0} \\ $$$${cos}^{\mathrm{2}} {B}+\mathrm{2}{cos}^{\mathrm{2}} {A}=\mathrm{0} \\ $$
Commented by mondodotto@gmail.com last updated on 07/Aug/18
thanx
$$\mathrm{thanx} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Aug/18
its ok...
$${its}\:{ok}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *