Question Number 168118 by Mastermind last updated on 03/Apr/22
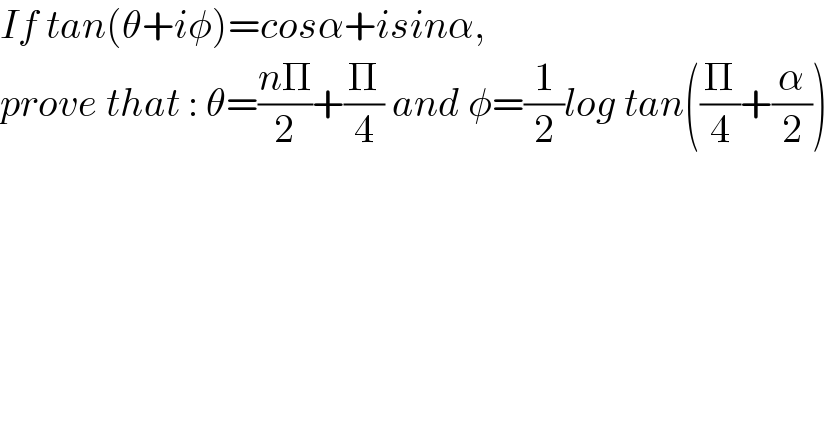
$${If}\:{tan}\left(\theta+{i}\phi\right)={cos}\alpha+{isin}\alpha,\: \\ $$$${prove}\:{that}\::\:\theta=\frac{{n}\Pi}{\mathrm{2}}+\frac{\Pi}{\mathrm{4}}\:{and}\:\phi=\frac{\mathrm{1}}{\mathrm{2}}{log}\:{tan}\left(\frac{\Pi}{\mathrm{4}}+\frac{\alpha}{\mathrm{2}}\right) \\ $$
Answered by mathsmine last updated on 05/Apr/22

$${tan}\left(\theta+{i}\emptyset\right)=\frac{{tan}\left(\theta\right)+{tan}\left({i}\emptyset\right)}{\mathrm{1}−{tan}\left(\theta\right){tan}\left({i}\emptyset\right)} \\ $$$${tan}\left({ix}\right)={ith}\left({x}\right) \\ $$$$\Leftrightarrow\frac{{tan}\left(\theta\right)+{ith}\left(\emptyset\right)}{\mathrm{1}−{itan}\left(\theta\right){th}\left(\emptyset\right)}={cos}\left({a}\right)+{isin}\left({a}\right) \\ $$$$\Leftrightarrow{cos}\left({a}\right)+{sin}\left({a}\right){tan}\left(\theta\right){th}\left(\emptyset\right)+{i}\left({sin}\left({a}\right)−{tan}\left(\theta\right){th}\left(\emptyset\right){cos}\left({a}\right)\right) \\ $$$$={tan}\left(\theta\right)+{ith}\left(\emptyset\right) \\ $$$${tan}\left(\theta\right)=\frac{{cos}\left({a}\right)}{\mathrm{1}−{sin}\left({a}\right){th}\left(\emptyset\right)} \\ $$$${th}\left(\emptyset\right)=\frac{{sin}\left({a}\right)}{\mathrm{1}+{tg}\left(\theta\right){cos}\left({a}\right)} \\ $$$$\Rightarrow{tg}\left(\theta\right)={cos}\left({a}\right)\left(\mathrm{1}+{tg}\left(\theta\right){cos}\left({a}\right)\right).\frac{\mathrm{1}}{\left(\mathrm{1}+{tg}\left(\theta\right){cos}\left({a}\right)−{sin}^{\mathrm{2}} \left({a}\right)\right.} \\ $$$$=\frac{\mathrm{1}+{tg}\left(\theta\right){cos}\left({a}\right)}{{tg}\left(\theta\right)+{cos}\left({a}\right)}\Leftrightarrow \\ $$$${tg}^{\mathrm{2}} \left(\theta\right)=\mathrm{1}\Rightarrow\:{tg}\left(\theta\right)=\underset{−} {+}\mathrm{1}\Rightarrow \\ $$$$\theta=\frac{\pi}{\mathrm{4}}+{n}\frac{\pi}{\mathrm{2}} \\ $$$${th}\left(\emptyset\right)=\frac{{sin}\left({a}\right)}{\mathrm{1}\underset{−} {+}{cos}\left({a}\right)}, \\ $$$$\frac{{sin}\left({a}\right)}{\mathrm{1}+{cos}\left({a}\right)}={tg}\left(\frac{{a}}{\mathrm{2}}\right)…..{E} \\ $$$$\frac{{sin}\left({a}\right)}{\mathrm{1}−{cos}\left({a}\right)}={cot}\left(\frac{{a}}{\mathrm{2}}\right) \\ $$$${th}\left({x}\right)={a}\Rightarrow{x}={argth}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{a}+\mathrm{1}}{\mathrm{1}−{a}}\right) \\ $$$${E}\Rightarrow\emptyset=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{tg}\left(\frac{{a}}{\mathrm{2}}\right)}{\left.\mathrm{1}−{tg}\left(\frac{{a}}{\mathrm{2}}\right)\right)}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({tg}\left(\frac{\pi}{\mathrm{4}}+\frac{{a}}{\mathrm{2}}\right)\right) \\ $$$$\leqslant\frac{\mathrm{1}+{tg}\left({x}\right)}{\mathrm{1}−{tg}\left({x}\right)}={tg}\left({x}+\frac{\pi}{\mathrm{4}}\right)\geqslant \\ $$$${So}\:\theta=\frac{{n}\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{4}} \\ $$$$\emptyset=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({tg}\left(\frac{{a}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Mastermind last updated on 05/Apr/22
$${Thanks}\:{man},\:{you}\:{did}\:{a}\:{great}\:{Job}! \\ $$$$ \\ $$$${Could}\:{you}\:{please}\:{drop}\:{your}\:{Whatsapp}\:{number}? \\ $$
