if-tan-r-s-and-sin-s-r-show-that-cos-r-2-s-

Question Number 33466 by mondodotto@gmail.com last updated on 17/Apr/18

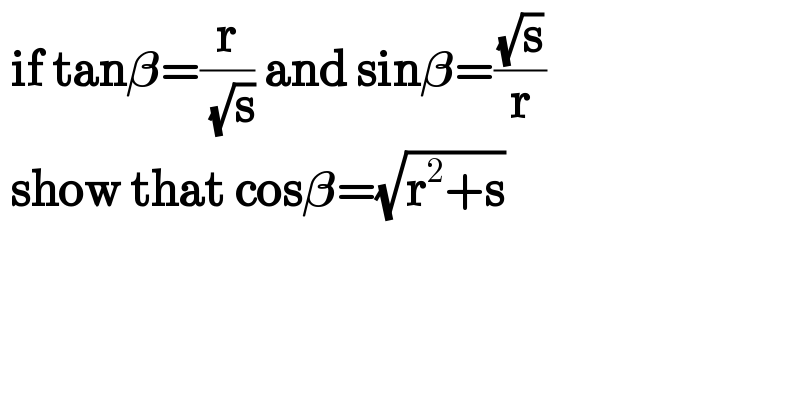
if tan𝛃=(r/( (√s))) and sin𝛃=((√s)/r) show that cos𝛃=(√(r^2 +s))

$$\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{tan}\beta}=\frac{\boldsymbol{\mathrm{r}}}{\:\sqrt{\boldsymbol{\mathrm{s}}}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{sin}\beta}=\frac{\sqrt{\boldsymbol{\mathrm{s}}}}{\boldsymbol{\mathrm{r}}} \\ $$$$\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}}\:\boldsymbol{\mathrm{cos}\beta}=\sqrt{\boldsymbol{\mathrm{r}}^{\mathrm{2}} +\boldsymbol{\mathrm{s}}} \\ $$

Commented by MJS last updated on 17/Apr/18

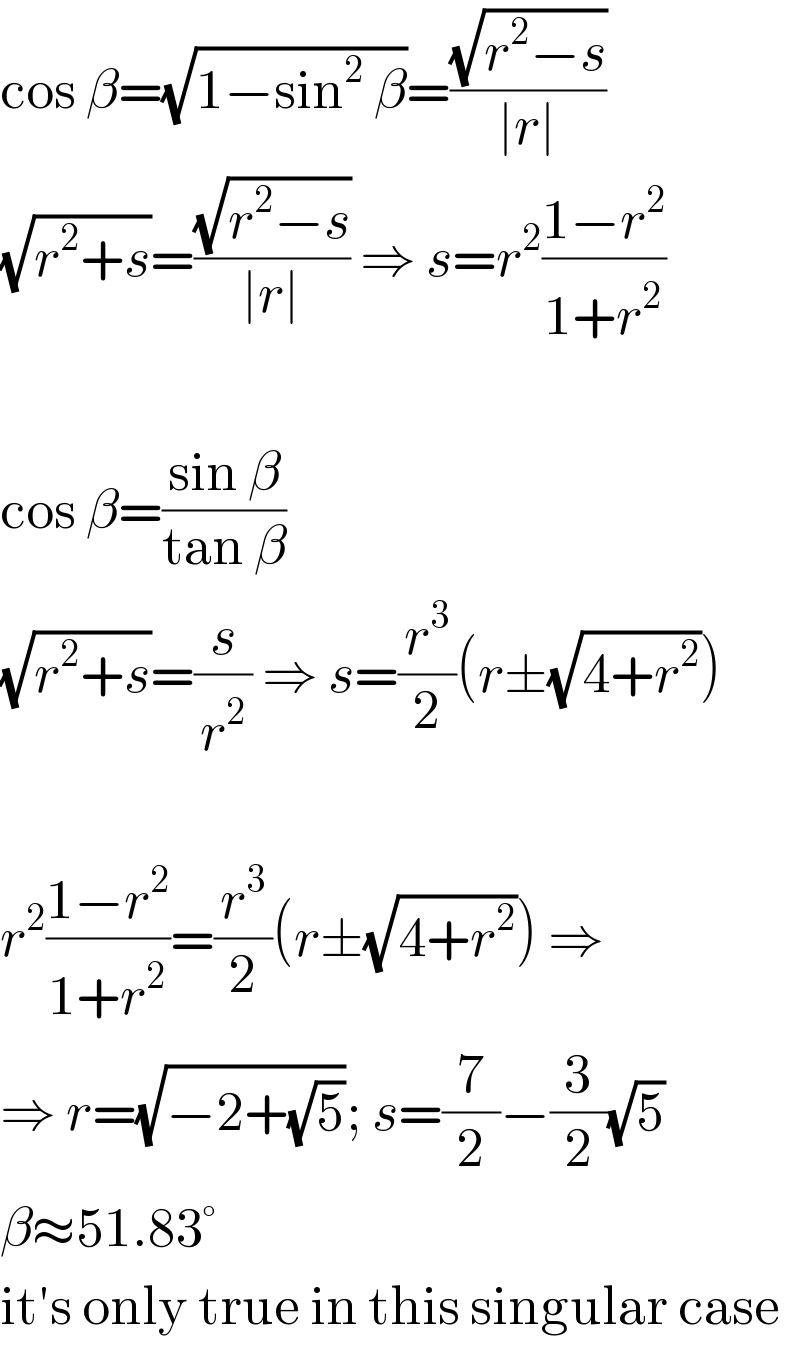
cos β=(√(1−sin^2 β))=((√(r^2 −s))/(∣r∣)) (√(r^2 +s))=((√(r^2 −s))/(∣r∣)) ⇒ s=r^2 ((1−r^2 )/(1+r^2 )) cos β=((sin β)/(tan β)) (√(r^2 +s))=(s/r^2 ) ⇒ s=(r^3 /2)(r±(√(4+r^2 ))) r^2 ((1−r^2 )/(1+r^2 ))=(r^3 /2)(r±(√(4+r^2 ))) ⇒ ⇒ r=(√(−2+(√5))); s=(7/2)−(3/2)(√5) β≈51.83° it′s only true in this singular case

$$\mathrm{cos}\:\beta=\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\beta}=\frac{\sqrt{{r}^{\mathrm{2}} −{s}}}{\mid{r}\mid} \\ $$$$\sqrt{{r}^{\mathrm{2}} +{s}}=\frac{\sqrt{{r}^{\mathrm{2}} −{s}}}{\mid{r}\mid}\:\Rightarrow\:{s}={r}^{\mathrm{2}} \frac{\mathrm{1}−{r}^{\mathrm{2}} }{\mathrm{1}+{r}^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{cos}\:\beta=\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\beta} \\ $$$$\sqrt{{r}^{\mathrm{2}} +{s}}=\frac{{s}}{{r}^{\mathrm{2}} }\:\Rightarrow\:{s}=\frac{{r}^{\mathrm{3}} }{\mathrm{2}}\left({r}\pm\sqrt{\mathrm{4}+{r}^{\mathrm{2}} }\right) \\ $$$$ \\ $$$${r}^{\mathrm{2}} \frac{\mathrm{1}−{r}^{\mathrm{2}} }{\mathrm{1}+{r}^{\mathrm{2}} }=\frac{{r}^{\mathrm{3}} }{\mathrm{2}}\left({r}\pm\sqrt{\mathrm{4}+{r}^{\mathrm{2}} }\right)\:\Rightarrow\: \\ $$$$\Rightarrow\:{r}=\sqrt{−\mathrm{2}+\sqrt{\mathrm{5}}};\:{s}=\frac{\mathrm{7}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{5}} \\ $$$$\beta\approx\mathrm{51}.\mathrm{83}° \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{only}\:\mathrm{true}\:\mathrm{in}\:\mathrm{this}\:\mathrm{singular}\:\mathrm{case} \\ $$

Commented by mondodotto@gmail.com last updated on 17/Apr/18

$$\mathrm{thanx}\:\mathrm{for}\:\mathrm{your}\:\mathrm{help}\:\mathrm{sir} \\ $$

Answered by Rasheed.Sindhi last updated on 17/Apr/18

tan𝛃=((sin𝛃)/(cos𝛃)) (r/( (√s)))=(((√s)/r)/(cos𝛃)) cos𝛃=(((√s)/r)/(r/( (√s))))=((√s)/r)×((√s)/r)=(s/r^2 )≠(√(r^2 +s)) in general.

$$\boldsymbol{\mathrm{tan}\beta}=\frac{\boldsymbol{\mathrm{sin}\beta}}{\boldsymbol{\mathrm{cos}\beta}} \\ $$$$ \\ $$$$\frac{\boldsymbol{\mathrm{r}}}{\:\sqrt{\boldsymbol{\mathrm{s}}}}=\frac{\frac{\sqrt{\boldsymbol{\mathrm{s}}}}{\boldsymbol{\mathrm{r}}}}{\boldsymbol{\mathrm{cos}\beta}} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{cos}\beta}=\frac{\frac{\sqrt{\boldsymbol{\mathrm{s}}}}{\boldsymbol{\mathrm{r}}}}{\frac{\boldsymbol{\mathrm{r}}}{\:\sqrt{\boldsymbol{\mathrm{s}}}}}=\frac{\sqrt{\boldsymbol{\mathrm{s}}}}{\boldsymbol{\mathrm{r}}}×\frac{\sqrt{\mathrm{s}}}{\mathrm{r}}=\frac{\mathrm{s}}{\mathrm{r}^{\mathrm{2}} }\neq\sqrt{\boldsymbol{\mathrm{r}}^{\mathrm{2}} +\boldsymbol{\mathrm{s}}}\:\mathrm{in}\:\mathrm{general}. \\ $$

Facebook Tweet Pin

if-tan-r-s-and-sin-s-r-show-that-cos-r-2-s-

Leave a Reply Cancel reply