If-tan-z-2-find-the-value-of-z-

Question Number 54093 by Tawa1 last updated on 28/Jan/19

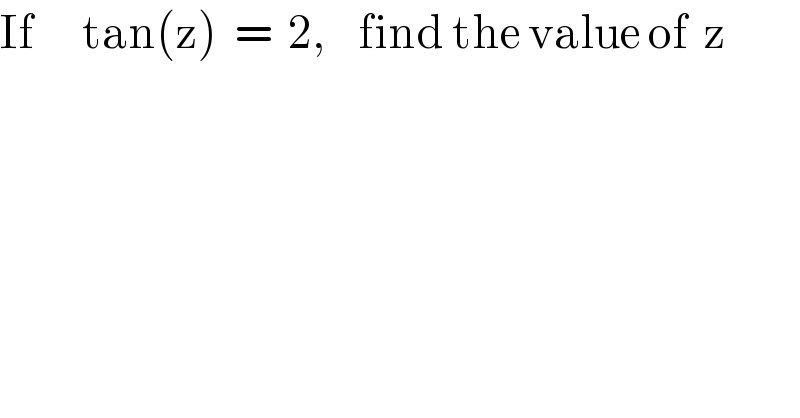
If \tan (z) = 2, find the value of z

Commented by mr W last updated on 28/Jan/19

z = \tan^{- 1} 2 + n π

Commented by Tawa1 last updated on 29/Jan/19

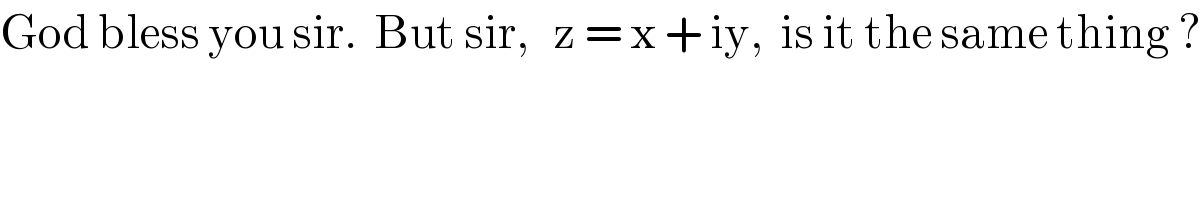
God bless you sir . But sir, z = x + iy, is it the same thing ?

Commented by mr W last updated on 29/Jan/19

z = x + y i

\tan z = \frac{\sin (2 x) + i \sinh (2 y)}{\cosh (2 y) + \cos (2 x)} = 2

\sinh (2 y) = 0 \Rightarrow y = 0

\sin (2 x) = 2 [\cosh (2 y) + \cos (2 x)]

2 \sin x \cos x = 2 [1 + {2 \cos}^{2} x - 1]

\sin x = 2 \cos x

\tan x = 2 \Rightarrow x = \tan^{- 1} 2 + n π

\Rightarrow z = \tan^{- 1} 2 + n π + 0 i

Commented by Tawa1 last updated on 29/Jan/19

God bless you sir, i appreciate .

Commented by Tawa1 last updated on 29/Jan/19

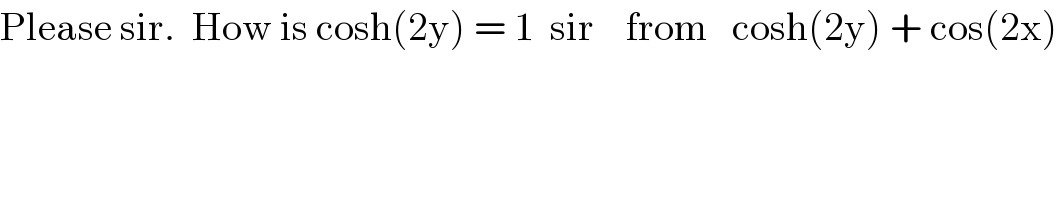
Please sir . How is \cosh (2 y) = 1 sir from \cosh (2 y) + \cos (2 x)

Commented by Tawa1 last updated on 29/Jan/19

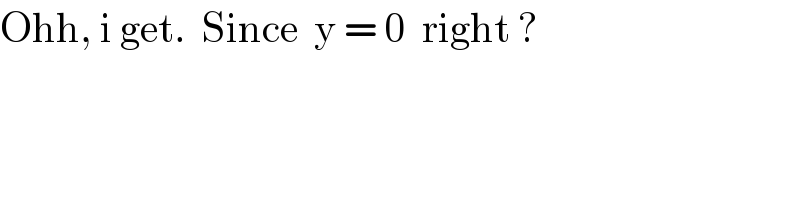
Ohh, i get . Since y = 0 right ?

Commented by mr W last updated on 29/Jan/19

y e s

Commented by Tawa1 last updated on 29/Jan/19

Thanks sir

Facebook Tweet Pin