Question Number 126405 by amns last updated on 20/Dec/20

$$\boldsymbol{\mathrm{If}}\:{tanA}\:=\:\sqrt{\mathrm{3}}\:,\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{it}}:\:\sqrt{\mathrm{3}}\:{sinA}\:{cosA}\:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by amns last updated on 20/Dec/20

$$\mathrm{help}\:\mathrm{me},\:\mathrm{plz}… \\ $$
Commented by som(math1967) last updated on 20/Dec/20
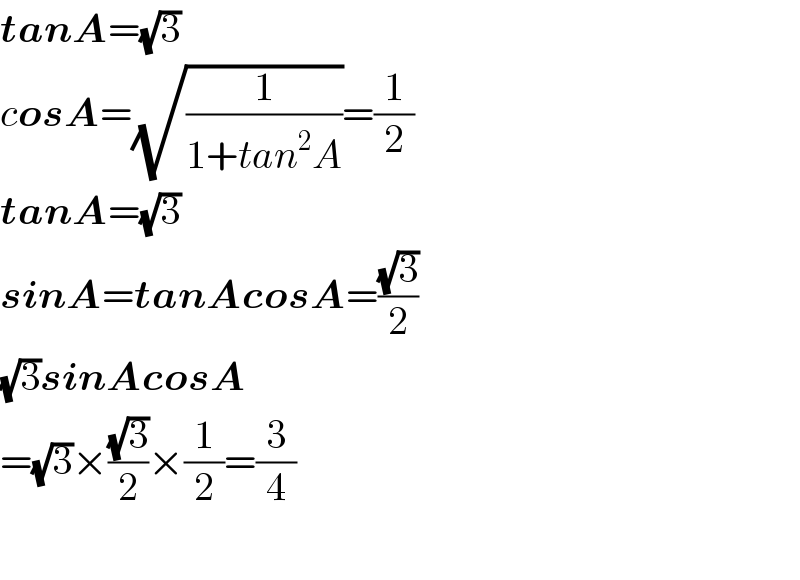
$$\boldsymbol{{tanA}}=\sqrt{\mathrm{3}} \\ $$$${c}\boldsymbol{{osA}}=\sqrt{\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} {A}}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\boldsymbol{{tanA}}=\sqrt{\mathrm{3}} \\ $$$$\boldsymbol{{sinA}}=\boldsymbol{{tanAcosA}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{3}}\boldsymbol{{sinAcosA}} \\ $$$$=\sqrt{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by benjo_mathlover last updated on 20/Dec/20
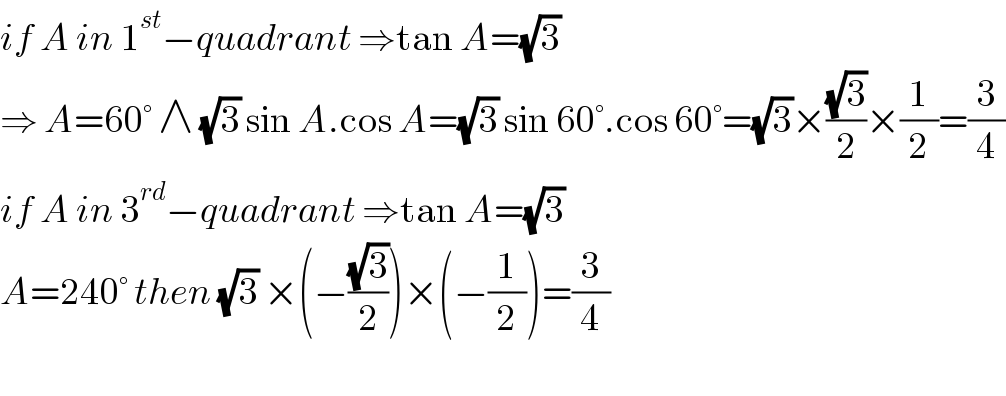
$${if}\:{A}\:{in}\:\mathrm{1}^{{st}} −{quadrant}\:\Rightarrow\mathrm{tan}\:{A}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:{A}=\mathrm{60}°\:\wedge\:\sqrt{\mathrm{3}}\:\mathrm{sin}\:{A}.\mathrm{cos}\:{A}=\sqrt{\mathrm{3}}\:\mathrm{sin}\:\mathrm{60}°.\mathrm{cos}\:\mathrm{60}°=\sqrt{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${if}\:{A}\:{in}\:\mathrm{3}^{{rd}} −{quadrant}\:\Rightarrow\mathrm{tan}\:{A}=\sqrt{\mathrm{3}} \\ $$$${A}=\mathrm{240}°\:{then}\:\sqrt{\mathrm{3}}\:×\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)×\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by TITA last updated on 20/Dec/20

$$\mathrm{tan}\:\mathrm{A}=\sqrt{\mathrm{3}}\:\:\:\mathrm{we}\:\mathrm{show}\:\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{Acos}\:\mathrm{A}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{A}=\mathrm{sin}\:\mathrm{A}\:\:\Rightarrow\:\mathrm{let}\:\mathrm{t}=\sqrt{\mathrm{3}}\mathrm{sin}\:\mathrm{Acos}\:\mathrm{A}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{A} \\ $$$$\Rightarrow\:\mathrm{t}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{A}=\frac{\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{A}}=\frac{\mathrm{3}}{\mathrm{1}+\mathrm{3}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 20/Dec/20
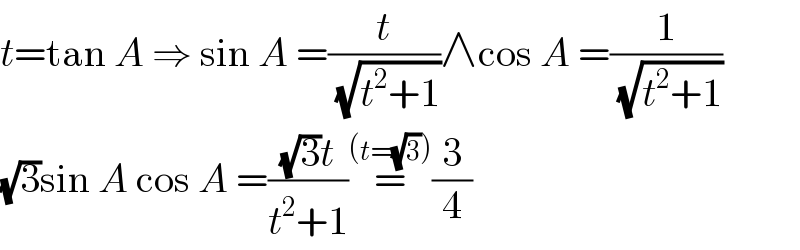
$${t}=\mathrm{tan}\:{A}\:\Rightarrow\:\mathrm{sin}\:{A}\:=\frac{{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\wedge\mathrm{cos}\:{A}\:=\frac{\mathrm{1}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\sqrt{\mathrm{3}}\mathrm{sin}\:{A}\:\mathrm{cos}\:{A}\:=\frac{\sqrt{\mathrm{3}}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\overset{\left({t}=\sqrt{\mathrm{3}}\right)} {=}\frac{\mathrm{3}}{\mathrm{4}} \\ $$
