Question Number 126702 by Eric002 last updated on 30/Dec/20
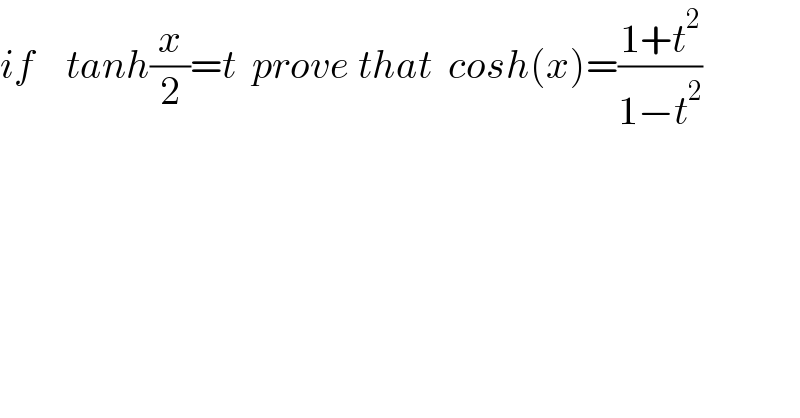
$${if}\:\:\:\:{tanh}\frac{{x}}{\mathrm{2}}={t}\:\:{prove}\:{that}\:\:{cosh}\left({x}\right)=\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by MJS_new last updated on 23/Dec/20

$$\mathrm{tanh}\:\alpha\:=\frac{\mathrm{e}^{\mathrm{2}\alpha} −\mathrm{1}}{\mathrm{e}^{\mathrm{2}\alpha} +\mathrm{1}}\wedge\mathrm{cosh}\:\alpha\:=\frac{\mathrm{e}^{\alpha} +\mathrm{e}^{−\alpha} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${t}=\mathrm{tanh}\:\frac{{x}}{\mathrm{2}}\:=\frac{\mathrm{e}^{{x}} −\mathrm{1}}{\mathrm{e}^{{x}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }=\frac{\mathrm{1}+\left(\frac{\mathrm{e}^{{x}} −\mathrm{1}}{\mathrm{e}^{{x}} +\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{1}−\left(\frac{\mathrm{e}^{{x}} −\mathrm{1}}{\mathrm{e}^{{x}} +\mathrm{1}}\right)^{\mathrm{2}} }=\frac{\frac{\left(\mathrm{e}^{{x}} +\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{e}^{{x}} +\mathrm{1}\right)^{\mathrm{2}} }}{\frac{\left(\mathrm{e}^{{x}} +\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{e}^{{x}} +\mathrm{1}\right)^{\mathrm{2}} }}= \\ $$$$=\frac{\mathrm{2e}^{\mathrm{2}{x}} +\mathrm{2}}{\mathrm{4e}^{{x}} }=\frac{\mathrm{e}^{{x}} +\mathrm{e}^{−{x}} }{\mathrm{2}}=\mathrm{cosh}\:{x} \\ $$
