Question Number 92225 by M±th+et+s last updated on 05/May/20
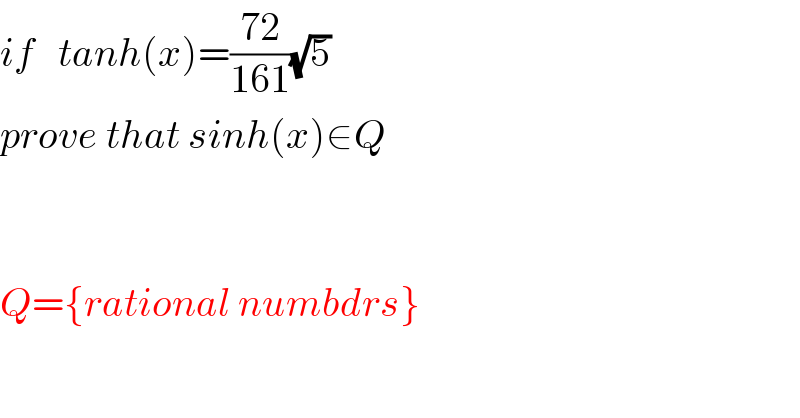
$${if}\:\:\:{tanh}\left({x}\right)=\frac{\mathrm{72}}{\mathrm{161}}\sqrt{\mathrm{5}} \\ $$$${prove}\:{that}\:{sinh}\left({x}\right)\in{Q}\: \\ $$$$ \\ $$$$ \\ $$$${Q}=\left\{{rational}\:{numbdrs}\right\} \\ $$$$ \\ $$
Answered by MJS last updated on 05/May/20
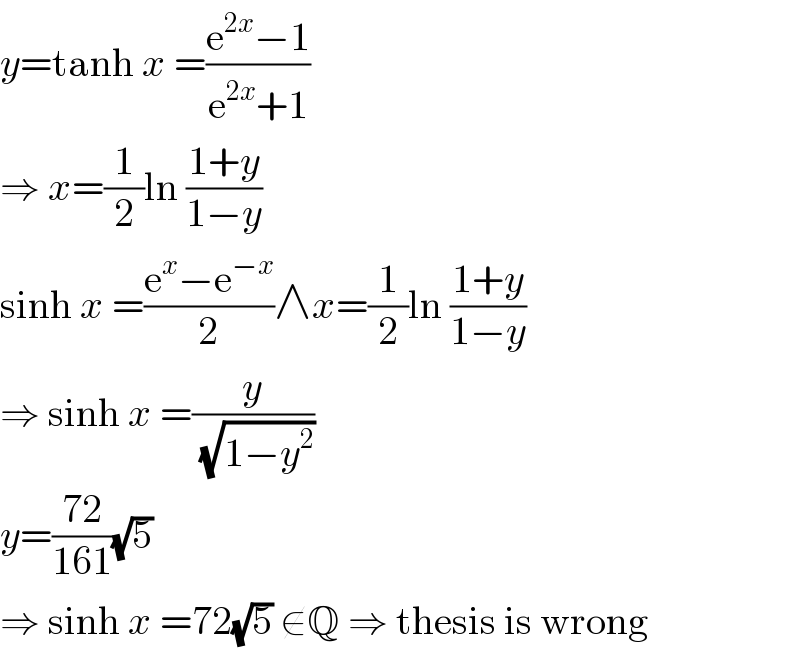
$${y}=\mathrm{tanh}\:{x}\:=\frac{\mathrm{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}} \\ $$$$\mathrm{sinh}\:{x}\:=\frac{\mathrm{e}^{{x}} −\mathrm{e}^{−{x}} }{\mathrm{2}}\wedge{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}} \\ $$$$\Rightarrow\:\mathrm{sinh}\:{x}\:=\frac{{y}}{\:\sqrt{\mathrm{1}−{y}^{\mathrm{2}} }} \\ $$$${y}=\frac{\mathrm{72}}{\mathrm{161}}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{sinh}\:{x}\:=\mathrm{72}\sqrt{\mathrm{5}}\:\notin\mathbb{Q}\:\Rightarrow\:\mathrm{thesis}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by M±th+et+s last updated on 05/May/20
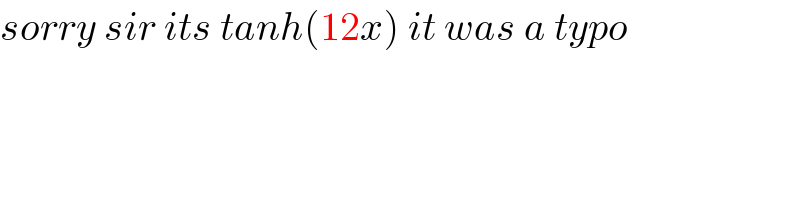
$${sorry}\:{sir}\:{its}\:{tanh}\left(\mathrm{12}{x}\right)\:{it}\:{was}\:{a}\:{typo}\: \\ $$
Commented by MJS last updated on 05/May/20

$$\mathrm{then}\:\mathrm{use}\:\mathrm{my}\:\mathrm{formulas}\:\mathrm{to}\:\mathrm{show}\:\mathrm{it}'\mathrm{s}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{btw}\:\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{5}} \\ $$
