If-the-area-enclosed-between-the-curves-y-x-and-the-line-y-2x-is-rotated-round-the-x-axis-through-4-right-angles-find-the-volume-of-the-solid-generated-

Question Number 184287 by Tawa11 last updated on 04/Jan/23

If the area enclosed between the curves y=x² and the line y = 2x is
rotated round the x-axis through 4 right angles, find the volume of
the solid generated

Answered by mr W last updated on 04/Jan/23

y_1 =2x y_2 =x^2 2x=x^2 ⇒x=0, x=2 V=∫_0 ^2 π(y_1 ^2 −y_2 ^2 )dx =∫_0 ^2 π(4x^2 −x^4 )dx =π[((4x^3 )/3)−(x^5 /5)]_0 ^2 =π(((4×8)/3)−((32)/5)) =((64π)/(15))

y_{1} = 2 x

y_{2} = x^{2}

2 x = x^{2} \Rightarrow x = 0, x = 2

V = \int_{0}^{2} π (y_{1}^{2} - y_{2}^{2}) d x

= \int_{0}^{2} π (4 x^{2} - x^{4}) d x

= π {[\frac{4 x^{3}}{3} - \frac{x^{5}}{5}]}_{0}^{2}

= π (\frac{4 \times 8}{3} - \frac{32}{5})

= \frac{64 π}{15}

Commented by Tawa11 last updated on 04/Jan/23

I appreciate sir .

Answered by mr W last updated on 04/Jan/23

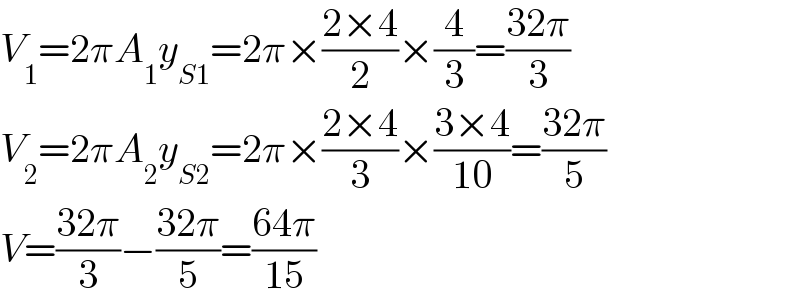
V_1 =2πA_1 y_(S1) =2π×((2×4)/2)×(4/3)=((32π)/3) V_2 =2πA_2 y_(S2) =2π×((2×4)/3)×((3×4)/(10))=((32π)/5) V=((32π)/3)−((32π)/5)=((64π)/(15))

V_{1} = 2 π A_{1} y_{S 1} = 2 π \times \frac{2 \times 4}{2} \times \frac{4}{3} = \frac{32 π}{3}

V_{2} = 2 π A_{2} y_{S 2} = 2 π \times \frac{2 \times 4}{3} \times \frac{3 \times 4}{10} = \frac{32 π}{5}

V = \frac{32 π}{3} - \frac{32 π}{5} = \frac{64 π}{15}

Commented by Tawa11 last updated on 05/Jan/23

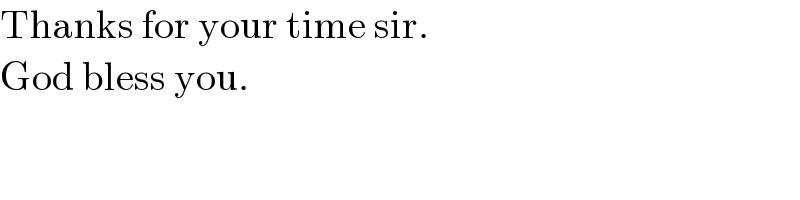
Thanks for your time sir. God bless you.

Thanks for your time sir .

God bless you .

Commented by Tawa11 last updated on 05/Jan/23

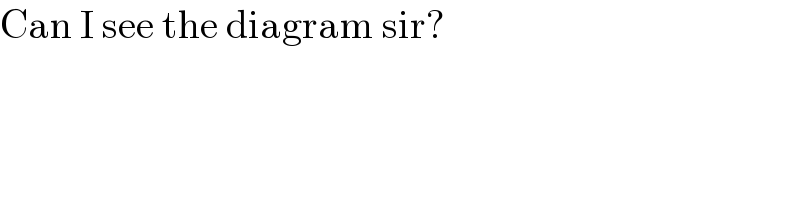
Can I see the diagram sir ?

Commented by mr W last updated on 05/Jan/23

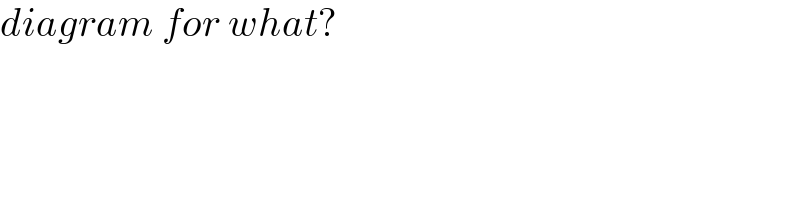
d i a g r a m f o r w h a t ?

Commented by Tawa11 last updated on 05/Jan/23

Graph I mean sir. For the volume as the area rotate. Is ut possible sir.

Graph I mean sir .

For the volume as the area rotate .

Is ut possible sir .

Commented by mr W last updated on 05/Jan/23

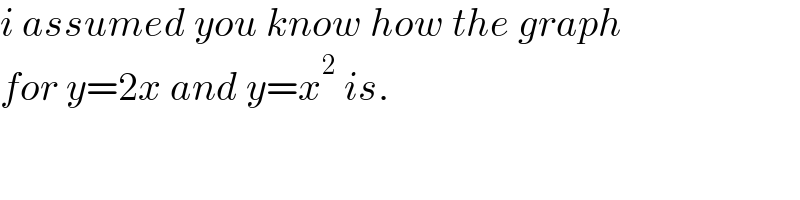
i assumed you know how the graph for y=2x and y=x^2 is.

i a s s u m e d y o u k n o w h o w t h e g r a p h

f o r y = 2 x a n d y = x^{2} i s .

Commented by Tawa11 last updated on 05/Jan/23

Yes sir . Very well .

Commented by mr W last updated on 05/Jan/23

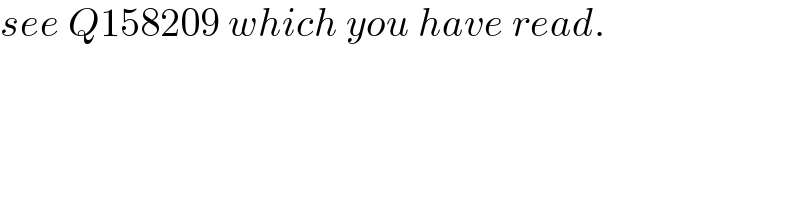
s e e Q 158209 w h i c h y o u h a v e r e a d .

Commented by Tawa11 last updated on 05/Jan/23

Seen sir, I understand now. God bless you sir.

Seen sir, I understand now .

God bless you sir .

Facebook Tweet Pin

If-the-area-enclosed-between-the-curves-y-x-and-the-line-y-2x-is-rotated-round-the-x-axis-through-4-right-angles-find-the-volume-of-the-solid-generated-

Leave a Reply Cancel reply