If-the-corrdinater-of-the-verticle-of-an-eqvilateral-triangle-with-length-x-are-x-1-y-1-y-1-y-2-and-x-3-y-3-then-determinant-x-1-y-1-2-x-2-y-2-2-x-3-y-3-2-

Tinku Tara June 4, 2023 Trigonometry 0 Comments

Question Number 32163 by jarjum last updated on 20/Mar/18

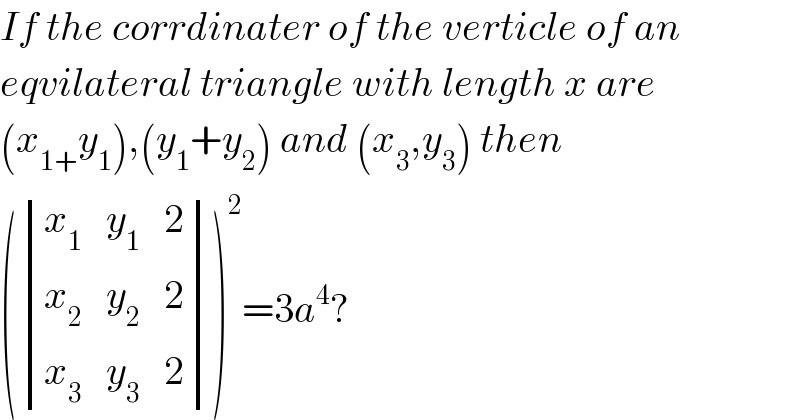
If the corrdinater of the verticle of an eqvilateral triangle with length x are (x_(1+) y_1 ),(y_1 +y_2 ) and (x_3 ,y_3 ) then ( determinant (((x_1 y_1 2)),((x_2 y_2 2)),((x_3 y_3 2))))^2 =3a^4 ?

$${If}\:{the}\:{corrdinater}\:{of}\:{the}\:{verticle}\:{of}\:{an} \\ $$$${eqvilateral}\:{triangle}\:{with}\:{length}\:{x}\:{are} \\ $$$$\left({x}_{\mathrm{1}+} {y}_{\mathrm{1}} \right),\left({y}_{\mathrm{1}} +{y}_{\mathrm{2}} \right)\:{and}\:\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} \right)\:{then} \\ $$$$\left(\begin{vmatrix}{{x}_{\mathrm{1}} \:\:\:{y}_{\mathrm{1}} \:\:\:\mathrm{2}}\\{{x}_{\mathrm{2}} \:\:\:{y}_{\mathrm{2}} \:\:\:\mathrm{2}}\\{{x}_{\mathrm{3}} \:\:\:{y}_{\mathrm{3}} \:\:\:\mathrm{2}}\end{vmatrix}\right)^{\mathrm{2}} =\mathrm{3}{a}^{\mathrm{4}} ? \\ $$

Facebook Tweet Pin

If-the-corrdinater-of-the-verticle-of-an-eqvilateral-triangle-with-length-x-are-x-1-y-1-y-1-y-2-and-x-3-y-3-then-determinant-x-1-y-1-2-x-2-y-2-2-x-3-y-3-2-

Leave a Reply Cancel reply