Question Number 20684 by Tinkutara last updated on 31/Aug/17
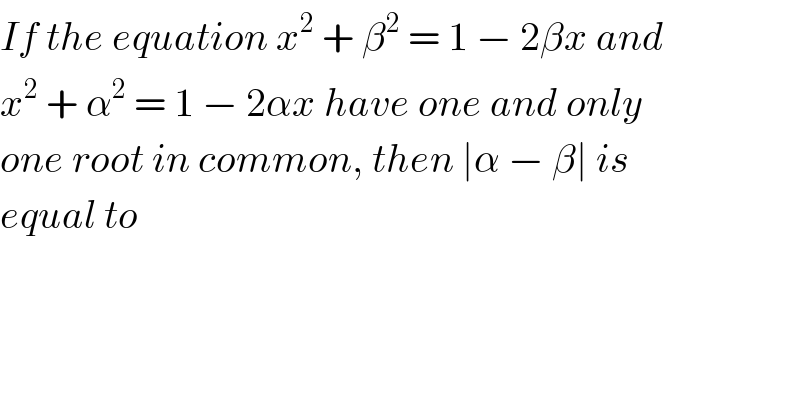
$${If}\:{the}\:{equation}\:{x}^{\mathrm{2}} \:+\:\beta^{\mathrm{2}} \:=\:\mathrm{1}\:−\:\mathrm{2}\beta{x}\:{and} \\ $$$${x}^{\mathrm{2}} \:+\:\alpha^{\mathrm{2}} \:=\:\mathrm{1}\:−\:\mathrm{2}\alpha{x}\:{have}\:{one}\:{and}\:{only} \\ $$$${one}\:{root}\:{in}\:{common},\:{then}\:\mid\alpha\:−\:\beta\mid\:{is} \\ $$$${equal}\:{to} \\ $$
Answered by $@ty@m last updated on 02/Sep/17

$${Let}\:{the}\:{common}\:{root}\:{be}\:{p} \\ $$$$\Rightarrow\left({p}+\alpha\right)^{\mathrm{2}} =\mathrm{1}\:\:\&\:\left({p}+\beta\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${Case}−{I}.\:{p}+\alpha=\mathrm{1},\:{p}+\beta=\mathrm{1} \\ $$$$\Rightarrow\alpha=\beta \\ $$$$\Rightarrow{both}\:{equations}\:{are}\:{same}. \\ $$$${Case}−{II}.\:{p}+\alpha=\mathrm{1}\:\&\:{p}+\beta=−\mathrm{1} \\ $$$$\Rightarrow\alpha−\beta=\mathrm{2} \\ $$$${Case}−{III}.{p}+\alpha=−\mathrm{1}\:\&\:{p}+\beta=\mathrm{1} \\ $$$$\Rightarrow−\left(\alpha−\beta\right)=\mathrm{2}\Rightarrow\left(\alpha−\beta\right)=−\mathrm{2} \\ $$$${Combining}\:{the}\:{results}\:{of}\:{Case}\:{II} \\ $$$${and}\:{Case}−{III},\:{we}\:{get} \\ $$$$\mid\alpha−\beta\mid=\mathrm{2} \\ $$
Commented by Tinkutara last updated on 02/Sep/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
