Question Number 33535 by NECx last updated on 18/Apr/18

$${If}\:{the}\:{frequency}\:{of}\:\mathrm{0}.\mathrm{75}\:{long}\:{simple} \\ $$$${pendulum}\:{is}\:\mathrm{1}.\mathrm{5}{Hz},{the}\:{angular} \\ $$$${frequency}\:{on}\:{a}\:{corresponding} \\ $$$${reference}\:{circle}\:{in}\:{rad}/{s}\:{is} \\ $$$$\left.{a}\left.\right)\left.\mathrm{1}\left..\mathrm{5}\pi\:{b}\right)\mathrm{3}\pi\:{c}\right)\mathrm{0}.\mathrm{5}\pi\:{d}\right)\mathrm{2}\pi \\ $$
Answered by ajfour last updated on 18/Apr/18
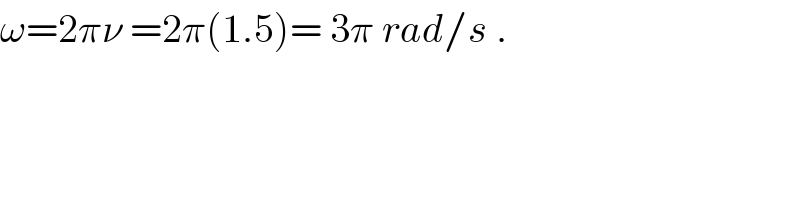
$$\omega=\mathrm{2}\pi\nu\:=\mathrm{2}\pi\left(\mathrm{1}.\mathrm{5}\right)=\:\mathrm{3}\pi\:{rad}/{s}\:. \\ $$
Commented by NECx last updated on 18/Apr/18
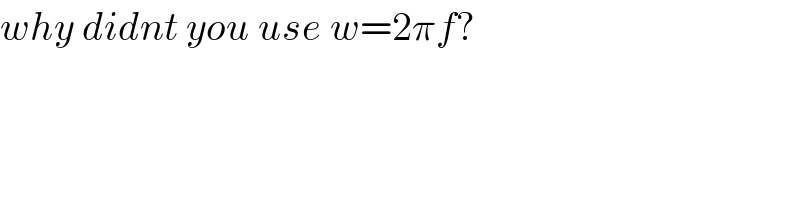
$${why}\:{didnt}\:{you}\:{use}\:{w}=\mathrm{2}\pi{f}? \\ $$
Commented by ajfour last updated on 19/Apr/18

$${symbol}\:{for}\:{frequency}-\:\:\:\nu\:{or}\:{f}\: \\ $$$${i}\:{used}\:\nu\:{for}\:{f}. \\ $$
