Question Number 168800 by MikeH last updated on 17/Apr/22
![If the function f is continuous in [a,b] express lim_(n→∞) (1/n)Σ_(k=1) ^n f((k/n)) as a definite integral.](https://www.tinkutara.com/question/Q168800.png)
$$\mathrm{If}\:\mathrm{the}\:\mathrm{function}\:{f}\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{in}\:\left[{a},{b}\right] \\ $$$$\mathrm{express}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left(\frac{{k}}{{n}}\right)\:\mathrm{as}\:\mathrm{a}\:\mathrm{definite} \\ $$$$\mathrm{integral}. \\ $$
Commented by safojontoshtemirov last updated on 18/Apr/22
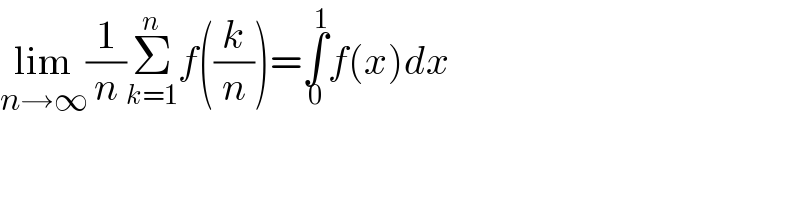
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{f}\left(\frac{{k}}{{n}}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx} \\ $$
