if-the-line-px-qy-r-tangents-the-ellipse-x-2-a-2-y-2-b-2-1-then-1-prove-a-2-p-2-b-2-q-2-r-2-2-find-the-coordinates-of-the-touching-point-

Question Number 157926 by mr W last updated on 29/Oct/21

i f t h e l i n e p x + q y = r t a n g e n t s t h e

e l l i p s e \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, t h e n

1) p r o v e a^{2} p^{2} + b^{2} q^{2} = r^{2}

2) f i n d t h e c o o r d i n a t e s o f t h e

t o u c h i n g p o i n t .

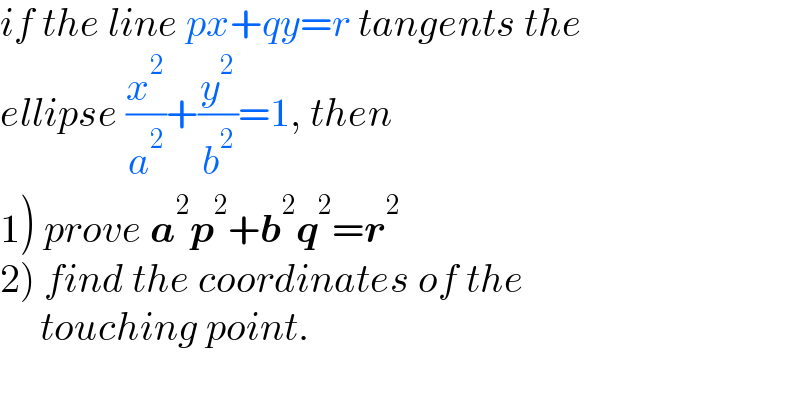
Answered by mindispower last updated on 29/Oct/21

\dots . p a r a m a t r i c o f e l i p s {(a c o s (t), b s i n (t))), t \in [0, 2 π [

M^{'} (t) = (- a s i n (t), b c o s (t))

M (t) \in L i n e p a c o s (t) + q b s i n (t) = r \dots (1)

M^{'} (t) d i r e c t o r v e c t o r a n d (- q, p) l i n e d i r e c t o r \Rightarrow

- q b c o s (t) + p a s i n (t) = 0 \dots

{(1)}^{2} + {(2)}^{2} \Leftrightarrow p^{2} a^{2} {c o s}^{2} (t) + q^{2} b^{2} {s i n}^{2} (t) + 2 p a q b s i n (t) c o s (t)

+ q^{2} b^{2} {c o s}^{2} (t) + p^{2} a^{2} {s i n}^{2} (t) - 2 a b p q s i n (t) c o s (t) = r^{2} + 0

\Leftrightarrow a^{2} p^{2} + b^{2} q^{2} = r^{2}

{\begin{cases} - q b c o s (t) + p a s i n (t) = 0 \dots . * s i n (t) . . 1 \\ p a c o s (t) + q b s i n (t) = r \dots \dots * c o s (t) \dots . 2 \end{cases}

(1) s i n (t) c o s (t) \neq 0

\Rightarrow (1) + (2) p a = r c o s (t) \Rightarrow c o s (t) = \frac{p a}{r}

M = (\frac{a^{2} p}{r}, \frac{b^{2} q}{r})

s i n (t) = \frac{q b}{r}

s i n (t) = 0 \Rightarrow - q b c o s (t) = 0, \Rightarrow q = 0

p a c o s (t) = r \Rightarrow c o s (t) = \frac{r}{p a} \Rightarrow∣ \frac{r}{p a} ∣= 1

i n t h i s c a s e t h e l i n e i s x = \frac{r}{p}, v e r t i c a l l i g n

M (\frac{r}{p}, 0)

c o s (t) = 0 \Rightarrow p = 0

s i n (t) = \frac{r}{q b} \dots \dots T h e l i g n i s y = \frac{r}{q} \overset{}{=} \underline{+} 1 v e r t i c a l l i n e

M (0, \frac{r}{q})

Commented by mr W last updated on 30/Oct/21

t h a n k s a l o t!

Commented by mindispower last updated on 02/Nov/21

p l e a s u r s i r h a v e a g o o d d a y

Answered by som(math1967) last updated on 30/Oct/21

p x + q y = r \Rightarrow y = \frac{r - p x}{q}

\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1

o r . \frac{x^{2}}{a^{2}} + \frac{{(r - p x)}^{2}}{b^{2} q^{2}} = 1

o r . x^{2} b^{2} q^{2} + a^{2} p^{2} x^{2} - 2 a^{2} p x r + r^{2} a^{2} = a^{2} b^{2} q^{2}

o r . (b^{2} q^{2} + a^{2} p^{2}) x^{2} - 2 a^{2} p x r + a^{2} r^{2} - a^{2} b^{2} q^{2} = 0 \dots 1)

p x + q y = r i s t a n g e n t s o f \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1

∴ {(- 2 a^{2} p r)}^{2} - 4 (b^{2} q^{2} + a^{2} p^{2}) (a^{2} r^{2} - a^{2} b^{2} q^{2}) = 0

[f o r e q u a l r o o t s d i s c r i m i n a n t i s 0]

4 a^{2} [a^{2} p^{2} r^{2} - (b^{2} q^{2} + a^{2} p^{2}) (r^{2} - b^{2} q^{2})] = 0

a^{2} p^{2} r^{2} - b^{2} q^{2} r^{2} + b^{4} q^{4} - a^{2} p^{2} r^{2} + a^{2} b^{2} p^{2} q^{2} = 0

b^{2} q^{2} (b^{2} q^{2} + a^{2} p^{2} - r^{2}) = 0

∴ a^{2} p^{2} + b^{2} q^{2} = r^{2}

f r o m e q u n . 1

(b^{2} q^{2} + a^{2} p^{2}) x^{2} - 2 a^{2} p x r + a^{2} r^{2} - a^{2} b^{2} q^{2} = 0

[(a^{2} p^{2} + b^{2} q^{2} = r^{2}]

r^{2} x^{2} - 2 a^{2} p x r + a^{2} (r^{2} - b^{2} q^{2}) = 0

r^{2} x^{2} - 2 . r x . a^{2} p + a^{4} . p^{2} = 0

x = \frac{a^{2} p}{r}

y = \frac{r - p x}{q} = \frac{r - \frac{a^{2} p^{2}}{r}}{q} = \frac{r^{2} - a^{2} p^{2}}{q r}

(\frac{a^{2} p}{r}, \frac{r^{2} - a^{2} p^{2}}{q r})

(\frac{a^{2} p}{r}, \frac{b^{2} q}{r})

Commented by mr W last updated on 30/Oct/21

t h a n k s a l o t!

Facebook Tweet Pin