Question Number 114879 by bobhans last updated on 21/Sep/20
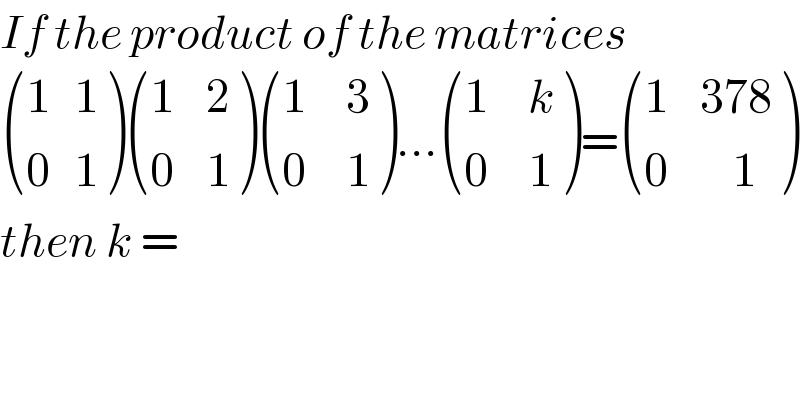
$${If}\:{the}\:{product}\:{of}\:{the}\:{matrices}\: \\ $$$$\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}…\begin{pmatrix}{\mathrm{1}\:\:\:\:\:{k}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{378}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${then}\:{k}\:=\: \\ $$
Answered by john santu last updated on 21/Sep/20

$$\left({i}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\left({ii}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{6}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\left({iii}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{6}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{4}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{10}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\left({iv}\right)\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{10}}\\{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{5}}\\{\mathrm{0}\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{15}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${therefore}\: \\ $$$$\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{1}}\\{\mathrm{0}\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{2}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{3}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}…\begin{pmatrix}{\mathrm{1}\:\:\:\:\:{k}}\\{\mathrm{0}\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\mathrm{378}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{k}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\mathrm{378}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$\Leftrightarrow\:\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{k}\:=\:\mathrm{378}\: \\ $$$$\:\:\:\:\frac{{k}\left({k}+\mathrm{1}\right)}{\mathrm{2}}\:=\:\mathrm{378}\:\Rightarrow{k}^{\mathrm{2}} +{k}−\mathrm{756}=\mathrm{0} \\ $$$$\:\:\:\:\left({k}+\mathrm{27}\right)\left({k}−\mathrm{28}\right)\:=\:\mathrm{0}\: \\ $$$$\:\:\Leftrightarrow\:{k}\:=\:\mathrm{28}\:. \\ $$
