Question Number 147010 by gsk2684 last updated on 17/Jul/21
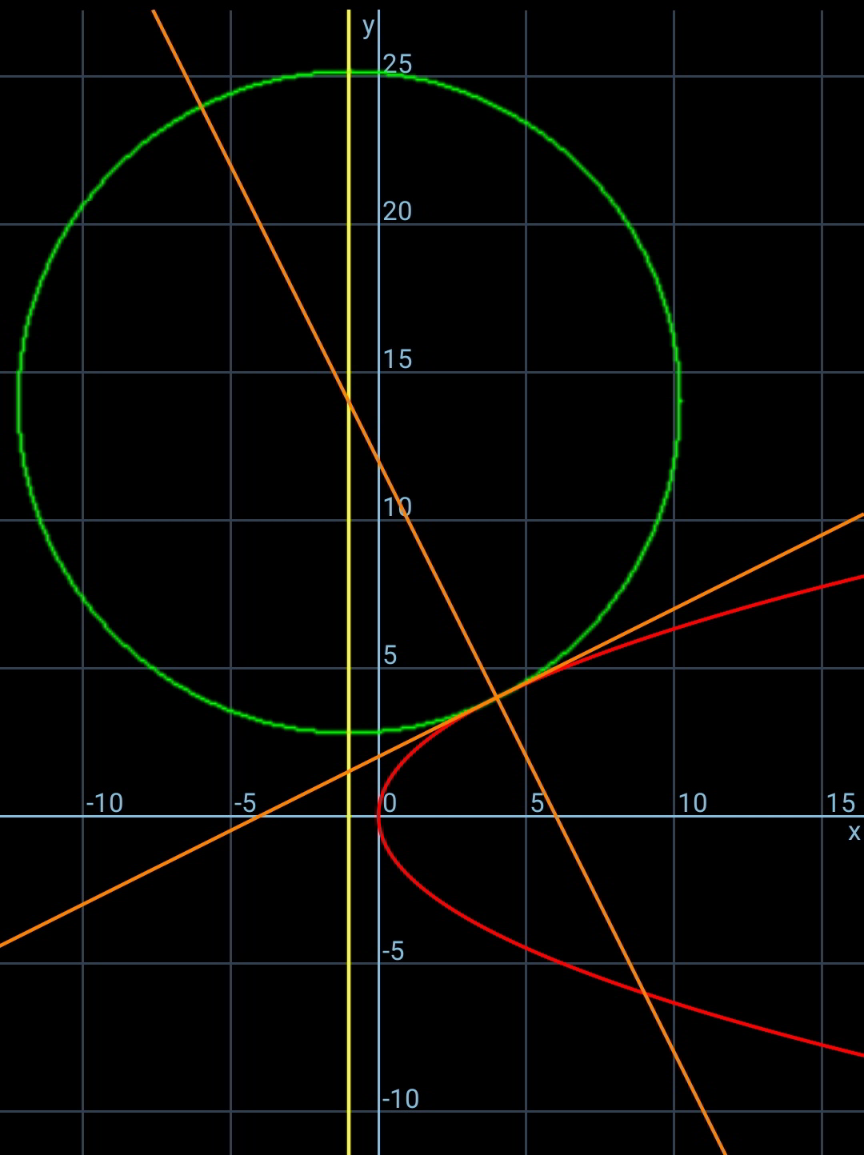
![if the radius of a circle touching parabola y^2 =4x at (4,4)and having directrix of y^2 =4x as its normal is r, then find [r]? (where [x] denote greatest integer lessthan or equal to x)](https://www.tinkutara.com/question/Q147010.png)
$${if}\:{the}\:{radius}\:{of}\:{a}\:{circle}\:{touching}\: \\ $$$${parabola}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:\:{at}\:\left(\mathrm{4},\mathrm{4}\right){and}\:{having} \\ $$$${directrix}\:{of}\:{y}^{\mathrm{2}} =\mathrm{4}{x}\:{as}\:{its}\:{normal}\: \\ $$$${is}\:{r},\:{then}\:{find}\:\left[{r}\right]? \\ $$$$\left({where}\:\left[{x}\right]\:{denote}\:{greatest}\:{integer}\:\right. \\ $$$$\left.{lessthan}\:{or}\:{equal}\:{to}\:{x}\right) \\ $$
Commented by gsk2684 last updated on 17/Jul/21
$${help}\:{me}\: \\ $$
Answered by mr W last updated on 17/Jul/21
![x=(y^2 /4) directrix is x=−1 (dx/dy)=(y/2) at (4,4): (dx/dy)=(4/2)=2 normal is y=4−2(x−4)=12−2x center of circle: x=−1 y=12−2(−1)=14 radius r: r^2 =(−1−4)^2 +(14−4)^2 =125 r=(√(125))>(√(121))=11, <(√(144))=12 ⇒[r]=11](https://www.tinkutara.com/question/Q147081.png)
$${x}=\frac{{y}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${directrix}\:{is}\:{x}=−\mathrm{1} \\ $$$$\frac{{dx}}{{dy}}=\frac{{y}}{\mathrm{2}} \\ $$$${at}\:\left(\mathrm{4},\mathrm{4}\right): \\ $$$$\frac{{dx}}{{dy}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2} \\ $$$${normal}\:{is} \\ $$$${y}=\mathrm{4}−\mathrm{2}\left({x}−\mathrm{4}\right)=\mathrm{12}−\mathrm{2}{x} \\ $$$${center}\:{of}\:{circle}: \\ $$$${x}=−\mathrm{1} \\ $$$${y}=\mathrm{12}−\mathrm{2}\left(−\mathrm{1}\right)=\mathrm{14} \\ $$$${radius}\:{r}: \\ $$$${r}^{\mathrm{2}} =\left(−\mathrm{1}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{14}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{125} \\ $$$${r}=\sqrt{\mathrm{125}}>\sqrt{\mathrm{121}}=\mathrm{11},\:<\sqrt{\mathrm{144}}=\mathrm{12} \\ $$$$\Rightarrow\left[{r}\right]=\mathrm{11} \\ $$
Commented by mr W last updated on 17/Jul/21
Commented by gsk2684 last updated on 18/Jul/21
$${thank}\:{you}\: \\ $$