Question Number 119396 by bemath last updated on 24/Oct/20
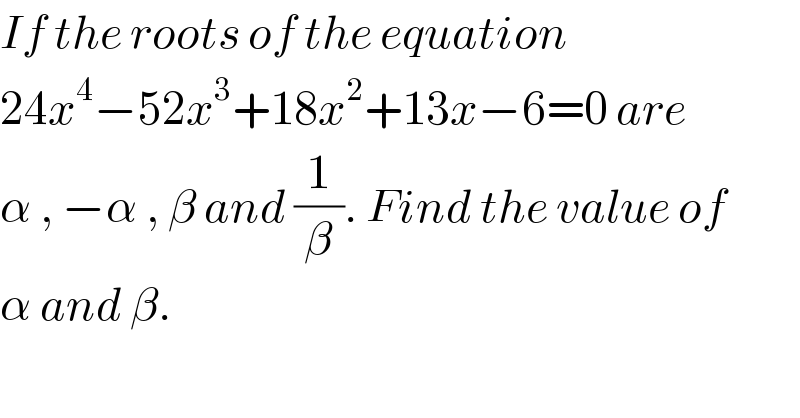
$${If}\:{the}\:{roots}\:{of}\:{the}\:{equation}\: \\ $$$$\mathrm{24}{x}^{\mathrm{4}} −\mathrm{52}{x}^{\mathrm{3}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}=\mathrm{0}\:{are}\: \\ $$$$\alpha\:,\:−\alpha\:,\:\beta\:{and}\:\frac{\mathrm{1}}{\beta}.\:{Find}\:{the}\:{value}\:{of}\: \\ $$$$\alpha\:{and}\:\beta. \\ $$
Commented by Dwaipayan Shikari last updated on 24/Oct/20
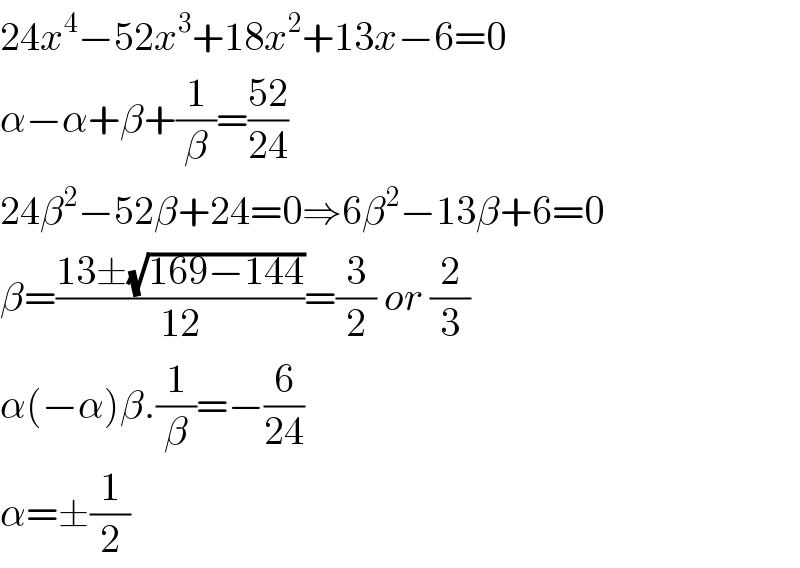
$$\mathrm{24}{x}^{\mathrm{4}} −\mathrm{52}{x}^{\mathrm{3}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}=\mathrm{0} \\ $$$$\alpha−\alpha+\beta+\frac{\mathrm{1}}{\beta}=\frac{\mathrm{52}}{\mathrm{24}} \\ $$$$\mathrm{24}\beta^{\mathrm{2}} −\mathrm{52}\beta+\mathrm{24}=\mathrm{0}\Rightarrow\mathrm{6}\beta^{\mathrm{2}} −\mathrm{13}\beta+\mathrm{6}=\mathrm{0} \\ $$$$\beta=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{144}}}{\mathrm{12}}=\frac{\mathrm{3}}{\mathrm{2}}\:{or}\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\alpha\left(−\alpha\right)\beta.\frac{\mathrm{1}}{\beta}=−\frac{\mathrm{6}}{\mathrm{24}} \\ $$$$\alpha=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 24/Oct/20
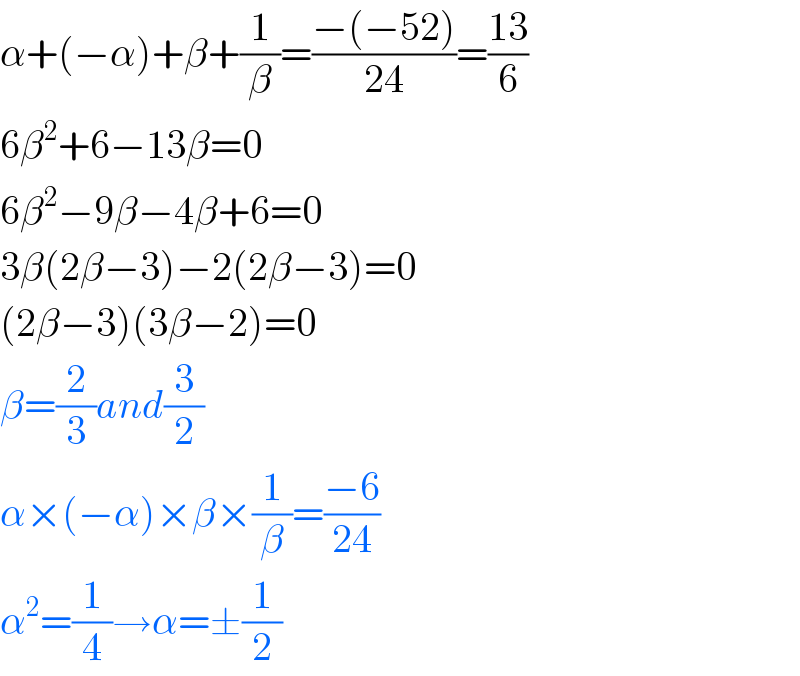
$$\alpha+\left(−\alpha\right)+\beta+\frac{\mathrm{1}}{\beta}=\frac{−\left(−\mathrm{52}\right)}{\mathrm{24}}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\mathrm{6}\beta^{\mathrm{2}} +\mathrm{6}−\mathrm{13}\beta=\mathrm{0} \\ $$$$\mathrm{6}\beta^{\mathrm{2}} −\mathrm{9}\beta−\mathrm{4}\beta+\mathrm{6}=\mathrm{0} \\ $$$$\mathrm{3}\beta\left(\mathrm{2}\beta−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}\beta−\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\mathrm{2}\beta−\mathrm{3}\right)\left(\mathrm{3}\beta−\mathrm{2}\right)=\mathrm{0} \\ $$$$\beta=\frac{\mathrm{2}}{\mathrm{3}}{and}\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\alpha×\left(−\alpha\right)×\beta×\frac{\mathrm{1}}{\beta}=\frac{−\mathrm{6}}{\mathrm{24}} \\ $$$$\alpha^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\rightarrow\alpha=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by $@y@m last updated on 24/Oct/20
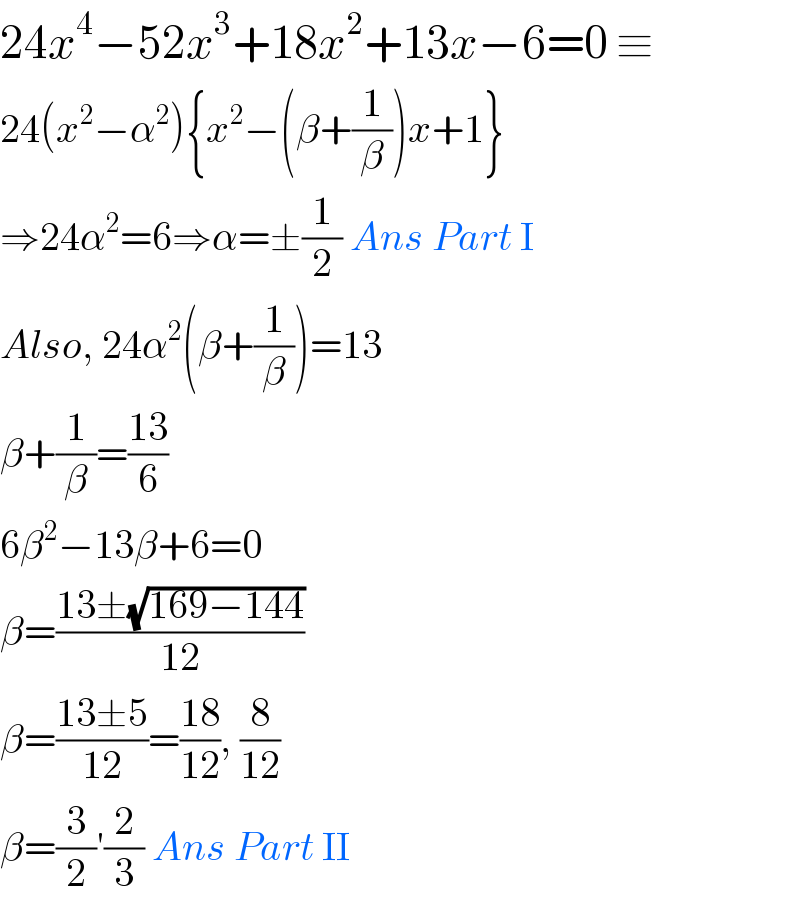
$$\mathrm{24}{x}^{\mathrm{4}} −\mathrm{52}{x}^{\mathrm{3}} +\mathrm{18}{x}^{\mathrm{2}} +\mathrm{13}{x}−\mathrm{6}=\mathrm{0}\:\equiv \\ $$$$\mathrm{24}\left({x}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)\left\{{x}^{\mathrm{2}} −\left(\beta+\frac{\mathrm{1}}{\beta}\right){x}+\mathrm{1}\right\} \\ $$$$\Rightarrow\mathrm{24}\alpha^{\mathrm{2}} =\mathrm{6}\Rightarrow\alpha=\pm\frac{\mathrm{1}}{\mathrm{2}}\:{Ans}\:{Part}\:\mathrm{I} \\ $$$${Also},\:\mathrm{24}\alpha^{\mathrm{2}} \left(\beta+\frac{\mathrm{1}}{\beta}\right)=\mathrm{13} \\ $$$$\beta+\frac{\mathrm{1}}{\beta}=\frac{\mathrm{13}}{\mathrm{6}} \\ $$$$\mathrm{6}\beta^{\mathrm{2}} −\mathrm{13}\beta+\mathrm{6}=\mathrm{0} \\ $$$$\beta=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{144}}}{\mathrm{12}} \\ $$$$\beta=\frac{\mathrm{13}\pm\mathrm{5}}{\mathrm{12}}=\frac{\mathrm{18}}{\mathrm{12}},\:\frac{\mathrm{8}}{\mathrm{12}} \\ $$$$\beta=\frac{\mathrm{3}}{\mathrm{2}}'\frac{\mathrm{2}}{\mathrm{3}}\:{Ans}\:{Part}\:\mathrm{II} \\ $$
Answered by 1549442205PVT last updated on 24/Oct/20
![24x^4 −52x^3 +18x^2 +13x−6 =24(x+α)(x−α)(x−β)(x−(1/β)) =24(x^2 −α^2 )[x^2 −(β+(1/β))x+1] =24{x^4 −[α^2 (β+(1/β))+β+(1/β)]x^3 +(1−α^2 )x^2 +α^2 (β+(1/β))x−α^2 } ⇔ { ((−24α^2 (β+(1/β))=−52(1))),((24(1−α^2 )=18(2))),((24α^2 (β+(1/β))=13(3))),((−24α^2 =−6(4))) :} (1)⇒α^2 =1/4⇒α=±1/2.Replace (1) (3)we get β+(1/β)=((13)/6)⇔6β^2 −13β+6=0 Δ=13^2 −144=25⇒β=((13±5)/(12))∈{(3/2),(2/3)} Thus,α=±(1/2),β∈{(3/2),(2/3)}](https://www.tinkutara.com/question/Q119413.png)
$$\mathrm{24x}^{\mathrm{4}} −\mathrm{52x}^{\mathrm{3}} +\mathrm{18x}^{\mathrm{2}} +\mathrm{13x}−\mathrm{6} \\ $$$$=\mathrm{24}\left(\mathrm{x}+\alpha\right)\left(\mathrm{x}−\alpha\right)\left(\mathrm{x}−\beta\right)\left(\mathrm{x}−\frac{\mathrm{1}}{\beta}\right) \\ $$$$=\mathrm{24}\left(\mathrm{x}^{\mathrm{2}} −\alpha^{\mathrm{2}} \right)\left[\mathrm{x}^{\mathrm{2}} −\left(\beta+\frac{\mathrm{1}}{\beta}\right)\mathrm{x}+\mathrm{1}\right] \\ $$$$=\mathrm{24}\left\{\mathrm{x}^{\mathrm{4}} −\left[\alpha^{\mathrm{2}} \left(\beta+\frac{\mathrm{1}}{\beta}\right)+\beta+\frac{\mathrm{1}}{\beta}\right]\mathrm{x}^{\mathrm{3}} \right. \\ $$$$\left.+\left(\mathrm{1}−\alpha^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} +\alpha^{\mathrm{2}} \left(\beta+\frac{\mathrm{1}}{\beta}\right)\mathrm{x}−\alpha^{\mathrm{2}} \right\} \\ $$$$\Leftrightarrow\begin{cases}{−\mathrm{24}\alpha^{\mathrm{2}} \left(\beta+\frac{\mathrm{1}}{\beta}\right)=−\mathrm{52}\left(\mathrm{1}\right)}\\{\mathrm{24}\left(\mathrm{1}−\alpha^{\mathrm{2}} \right)=\mathrm{18}\left(\mathrm{2}\right)}\\{\mathrm{24}\alpha^{\mathrm{2}} \left(\beta+\frac{\mathrm{1}}{\beta}\right)=\mathrm{13}\left(\mathrm{3}\right)}\\{−\mathrm{24}\alpha^{\mathrm{2}} =−\mathrm{6}\left(\mathrm{4}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)\Rightarrow\alpha^{\mathrm{2}} =\mathrm{1}/\mathrm{4}\Rightarrow\alpha=\pm\mathrm{1}/\mathrm{2}.\mathrm{Replace}\:\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get}\:\beta+\frac{\mathrm{1}}{\beta}=\frac{\mathrm{13}}{\mathrm{6}}\Leftrightarrow\mathrm{6}\beta^{\mathrm{2}} −\mathrm{13}\beta+\mathrm{6}=\mathrm{0} \\ $$$$\Delta=\mathrm{13}^{\mathrm{2}} −\mathrm{144}=\mathrm{25}\Rightarrow\beta=\frac{\mathrm{13}\pm\mathrm{5}}{\mathrm{12}}\in\left\{\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{2}}{\mathrm{3}}\right\} \\ $$$$\mathrm{Thus},\alpha=\pm\frac{\mathrm{1}}{\mathrm{2}},\beta\in\left\{\frac{\mathrm{3}}{\mathrm{2}},\frac{\mathrm{2}}{\mathrm{3}}\right\} \\ $$
