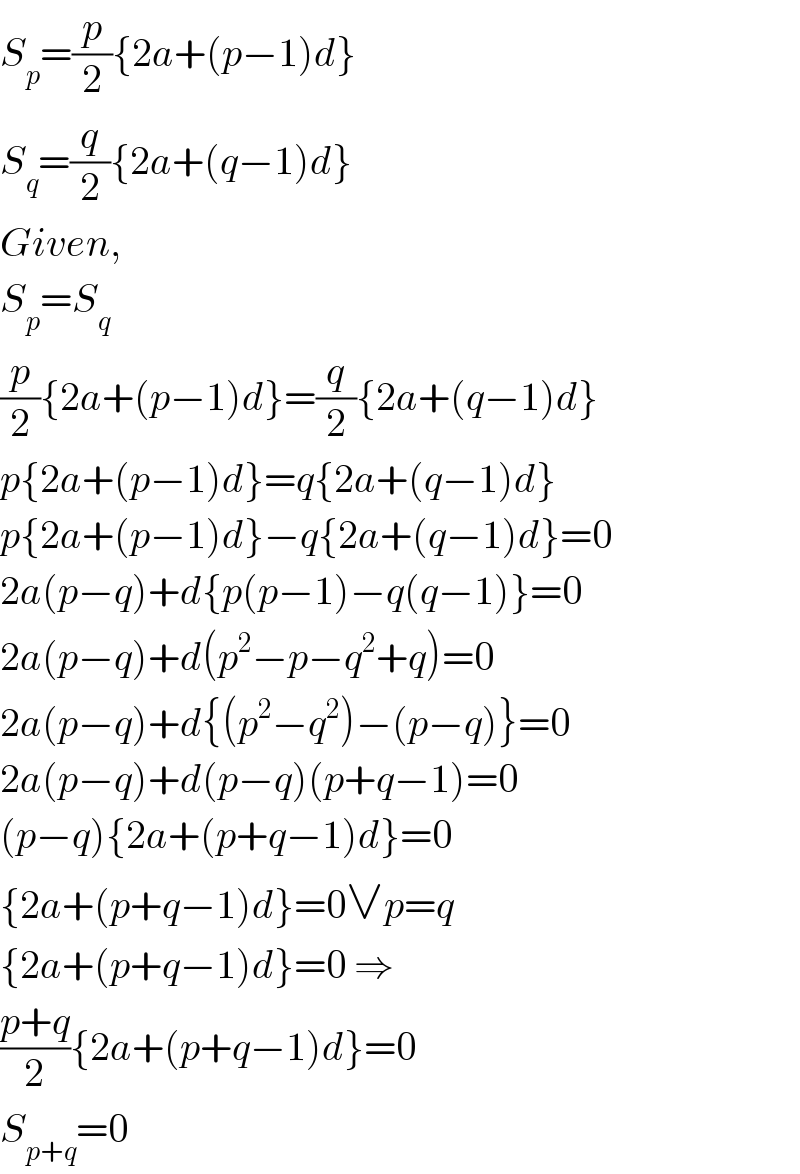IF-THE-SUM-OF-p-TERMS-OF-AN-A-P-IS-EQUAL-TO-SUM-OF-ITS-q-TERMS-PROVE-THAT-THE-SUM-OF-p-q-TERMS-OF-IT-IS-EQUAL-TO-0-ZERO-

Question Number 80159 by Mr. AR last updated on 31/Jan/20

I F T H E S U M O F p T E R M S

O F A N A . P . I S E Q U A L T O

S U M O F I T S q T E R M S .

P R O V E T H A T T H E S U M O F

(p + q) T E R M S O F I T I S

E Q U A L T O 0 (Z E R O) .

Commented by mr W last updated on 31/Jan/20

s e e m s i l l o g i c a l

Commented by Rio Michael last updated on 31/Jan/20

sir sum of p terms of an AP

and sum of q terms {don}^{'} t actually make

sense esspecially when the sum of

(p + q) terms are involved .

Commented by $@ty@m123 last updated on 31/Jan/20

E x a m p l e :

C o n s i d e r t h e f o l l o w i n g A . P .

1, \frac{1}{2}, 0, \frac{- 1}{2}, - 1

H e r e,

S_{2} = S_{3}

& S_{5} = 0

Commented by mr W last updated on 01/Feb/20

t h e q u e s t i o n {d i d n}^{'} t s a y t h e f i r s t p t e r m s,

t h e f i r s t q t e r m s a n d t h e f i r s t p + q

t e r m s .

Answered by $@ty@m123 last updated on 31/Jan/20

S_{p} = \frac{p}{2} {2 a + (p - 1) d}

S_{q} = \frac{q}{2} {2 a + (q - 1) d}

G i v e n,

S_{p} = S_{q}

\frac{p}{2} {2 a + (p - 1) d} = \frac{q}{2} {2 a + (q - 1) d}

p {2 a + (p - 1) d} = q {2 a + (q - 1) d}

p {2 a + (p - 1) d} - q {2 a + (q - 1) d} = 0

2 a (p - q) + d {p (p - 1) - q (q - 1)} = 0

2 a (p - q) + d (p^{2} - p - q^{2} + q) = 0

2 a (p - q) + d {(p^{2} - q^{2}) - (p - q)} = 0

2 a (p - q) + d (p - q) (p + q - 1) = 0

(p - q) {2 a + (p + q - 1) d} = 0

{2 a + (p + q - 1) d} = 0 \lor p = q

{2 a + (p + q - 1) d} = 0 \Rightarrow

\frac{p + q}{2} {2 a + (p + q - 1) d} = 0

S_{p + q} = 0