Question Number 90881 by M±th+et+s last updated on 26/Apr/20

$${if}\:{the}\:{value}\:{of}\:{x}\:{is}\:{in}\:{degrees}\:{what}\:{is} \\ $$$${the}\:{derivative}\:{of}\:\:\:{f}\left({x}\right)={sin}\left({x}\right) \\ $$
Commented by mr W last updated on 28/Apr/20
![we have different understanding: if x is in rad, the slope (dy/dx) is in unit [1/rad]. but if x is in degree, the slope is in unit [1/degree]. both slopes must not equal in value, but equal in the physical sense. when we describe the motion of a car with y=f(t)=sin(t) where t is in second, the slope (dy/dt) which is the speed in unit [m/s]. but if t is in mile, the slope (dy/dt) is also the speed, just in an other unit [m/mile]. both are of different values, but mean the same physical sense. t in f(t) can be in second or mile, x in sin(x) can be in rad or degree, which doen′t affect how we calculate (dy/dt) or (dy/dx). this is my understanding, maybe correct or maybe not.](https://www.tinkutara.com/question/Q91165.png)
$${we}\:{have}\:{different}\:{understanding}: \\ $$$${if}\:{x}\:{is}\:{in}\:{rad},\:{the}\:{slope}\:\frac{{dy}}{{dx}}\:{is}\:{in}\:{unit} \\ $$$$\left[\mathrm{1}/{rad}\right].\:{but}\:{if}\:{x}\:{is}\:{in}\:{degree},\:{the} \\ $$$${slope}\:{is}\:{in}\:{unit}\:\left[\mathrm{1}/{degree}\right].\:{both}\:{slopes} \\ $$$${must}\:{not}\:{equal}\:{in}\:{value},\:{but}\:{equal}\:{in} \\ $$$${the}\:{physical}\:{sense}. \\ $$$${when}\:{we}\:{describe}\:{the}\:{motion}\:{of}\:{a}\:{car} \\ $$$${with}\:{y}={f}\left({t}\right)={sin}\left({t}\right)\:{where}\:{t}\:{is}\:{in}\:{second}, \\ $$$${the}\:{slope}\:\frac{{dy}}{{dt}}\:{which}\:{is}\:{the}\:{speed}\:{in}\:{unit} \\ $$$$\left[{m}/{s}\right].\:{but}\:{if}\:{t}\:{is}\:{in}\:{mile},\:{the}\:{slope}\:\frac{{dy}}{{dt}} \\ $$$${is}\:{also}\:{the}\:{speed},\:{just}\:{in}\:{an}\:{other} \\ $$$${unit}\:\left[{m}/{mile}\right].\:{both}\:{are}\:{of}\:{different} \\ $$$${values},\:{but}\:{mean}\:{the}\:{same}\:{physical} \\ $$$${sense}.\:{t}\:{in}\:{f}\left({t}\right)\:{can}\:{be}\:{in}\:{second}\:{or}\:{mile}, \\ $$$${x}\:{in}\:{sin}\left({x}\right)\:{can}\:{be}\:{in}\:{rad}\:{or}\:{degree}, \\ $$$${which}\:{doen}'{t}\:{affect}\:{how}\:{we}\:{calculate} \\ $$$$\frac{{dy}}{{dt}}\:{or}\:\frac{{dy}}{{dx}}.\:{this}\:{is}\:{my}\:{understanding}, \\ $$$${maybe}\:{correct}\:{or}\:{maybe}\:{not}. \\ $$
Commented by mr W last updated on 26/Apr/20

$$\frac{{dy}}{{dx}}=\mathrm{cos}\:\left({x}\right)\:{no}\:{matter}\:{if}\:{x}\:{is}\:{in}\:{rad}\:{or} \\ $$$${in}\:{degree}. \\ $$$${this}\:{is}\:{the}\:{same}\:{as}\:{if}\:{s}={f}\left({t}\right), \\ $$$${v}=\frac{{ds}}{{dt}}={f}'\left({t}\right),\:{no}\:{matter}\:{if}\:{t}\:{is}\:{in}\:{hour} \\ $$$${or}\:{second}. \\ $$
Commented by M±th+et+s last updated on 26/Apr/20

$${thank}\:{you}\:{sir}\:{for}\:{explain}\:{that} \\ $$
Commented by MJS last updated on 26/Apr/20
![Sir, this obviuosly is wrong the derivate is the slope of the tangent (d/dx)[sin x^(rad) ]=cos x^(rad) but the slope of sin x° is not as steep (d/dx)[sin x°]=(π/(180))sin x° generally if f(x°) is any trigonometric function (d/dx)[f(x°)]=(π/(180))f′(x°)](https://www.tinkutara.com/question/Q90913.png)
$$\mathrm{Sir},\:\mathrm{this}\:\mathrm{obviuosly}\:\mathrm{is}\:\mathrm{wrong} \\ $$$$\mathrm{the}\:\mathrm{derivate}\:\mathrm{is}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent} \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{sin}\:{x}^{\mathrm{rad}} \right]=\mathrm{cos}\:{x}^{\mathrm{rad}} \\ $$$$\mathrm{but}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{sin}\:{x}°\:\mathrm{is}\:\mathrm{not}\:\mathrm{as}\:\mathrm{steep} \\ $$$$\frac{{d}}{{dx}}\left[\mathrm{sin}\:{x}°\right]=\frac{\pi}{\mathrm{180}}\mathrm{sin}\:{x}° \\ $$$$\mathrm{generally}\:\mathrm{if}\:{f}\left({x}°\right)\:\mathrm{is}\:\mathrm{any}\:\mathrm{trigonometric} \\ $$$$\mathrm{function} \\ $$$$\frac{{d}}{{dx}}\left[{f}\left({x}°\right)\right]=\frac{\pi}{\mathrm{180}}{f}'\left({x}°\right) \\ $$
Commented by mr W last updated on 26/Apr/20

$${if}\:{x}\:{in}\:{f}\left({x}\right)\:{is}\:{in}\:{degree},\:{then}\:{the}\:{x}\:{in}\: \\ $$$${dx}\:{is}\:{also}\:{in}\:{degree}. \\ $$$$ \\ $$$${say}\:{f}\left({x}\right)=\mathrm{sin}\:\left({x}\right)\:{with}\:{x}\:{in}\:{degree}. \\ $$$${t}=\frac{{x}\pi}{\mathrm{180}}\:\Rightarrow{x}=\frac{\mathrm{180}{t}}{\pi} \\ $$$$\frac{{d}\left(\mathrm{sin}\:{x}\right)}{{dx}}=\frac{{d}\left(\mathrm{sin}\:\frac{\mathrm{180}{t}}{\pi}\right)}{\frac{\mathrm{180}}{\pi}{dt}}=\frac{\left(\mathrm{cos}\:\frac{\mathrm{180}{t}}{\pi}\right)\frac{\mathrm{180}}{\pi}}{\frac{\mathrm{180}}{\pi}}=\mathrm{cos}\:\frac{\mathrm{180}{t}}{\pi}=\mathrm{cos}\:{x} \\ $$$${i}\:{think}\:{in}\:\frac{{dy}}{{dx}}\:{we}\:{see}\:{only}\:{function},\:{i}.{e}. \\ $$$${the}\:{math}.\:{relationship}\:{between}\:{y}\:{and}\:{x}, \\ $$$${we}\:{don}'{t}\:{care}\:{about}\:{the}\:{unit}\:{of}\:{y}\:{and}\:{x}. \\ $$
Commented by MJS last updated on 26/Apr/20

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true}.\:\mathrm{we}\:\mathrm{plot}\:\mathrm{the}\:\mathrm{function} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{coordinate}\:\mathrm{system}.\:\mathrm{if}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{is} \\ $$$$\mathrm{measured}\:\mathrm{in}\:\mathrm{radiants},\:\mathrm{the}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{sin}\:{x}\:\mathrm{at} \\ $$$${x}=\mathrm{0}\:\mathrm{is}\:\mathrm{1}.\:\mathrm{but}\:\mathrm{if}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{is}\:\mathrm{measured}\:\mathrm{in} \\ $$$$\mathrm{degree}\:\mathrm{the}\:\mathrm{slope}\:\mathrm{cannot}\:\mathrm{be}\:\mathrm{1}\:\mathrm{because} \\ $$$$\mathrm{now}\:\mathrm{the}\:\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\left(\mathrm{0}+{h}\right)\:−\mathrm{sin}\:\left(\mathrm{0}−{h}\right)}{\mathrm{2}{h}}\:=\frac{\pi}{\mathrm{180}} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{need}\:\mathrm{a}\:\mathrm{function}\:\mathrm{with}\:{f}\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{180}} \\ $$
Answered by TANMAY PANACEA. last updated on 26/Apr/20

$${x}\:{degree}=\frac{\pi}{\mathrm{180}}{x}\:{radian} \\ $$$${y}={sin}\left(\frac{\pi}{\mathrm{180}}{x}\right) \\ $$$$\frac{{dy}}{{dx}}={cos}\left(\frac{\pi}{\mathrm{180}}{x}\right)×\frac{\pi}{\mathrm{180}} \\ $$
Commented by M±th+et+s last updated on 26/Apr/20

$${thank}\:{you}\:{sir}\:{but}\:{i}\:{have}\:{a}\:{question} \\ $$$${why}\:\:{sin}\left(\frac{\pi}{\mathrm{180}}{x}\right)={sin}\left({x}\right)\: \\ $$$${but}\:\frac{\pi}{\mathrm{180}}{cos}\left(\frac{\pi}{\mathrm{180}}{x}\right)={cos}\left({x}\right) \\ $$$${because}\:{we}\:{know}\:\frac{{d}}{{dx}}{sin}\left({x}\right)={cos}\left({x}\right) \\ $$$$ \\ $$
Answered by M±th+et+s last updated on 27/Apr/20
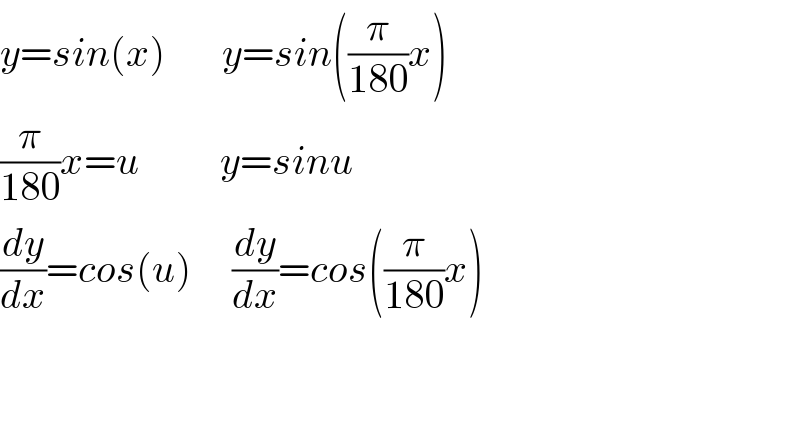
$${y}={sin}\left({x}\right)\:\:\:\:\:\:\:{y}={sin}\left(\frac{\pi}{\mathrm{180}}{x}\right) \\ $$$$\frac{\pi}{\mathrm{180}}{x}={u}\:\:\:\:\:\:\:\:\:\:{y}={sinu} \\ $$$$\frac{{dy}}{{dx}}={cos}\left({u}\right)\:\:\:\:\:\frac{{dy}}{{dx}}={cos}\left(\frac{\pi}{\mathrm{180}}{x}\right)\:\:\:\: \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 27/Apr/20

$$\frac{{dy}}{{dx}}{sin}\left({x}\right)={cos}\left({x}\right) \\ $$$${x}\:{rad}=\frac{\pi}{\mathrm{180}}{x}\:{deg} \\ $$$${cos}\left({x}\right)={cos}\left(\frac{\pi}{\mathrm{180}}{x}\right) \\ $$$${so}\:\frac{{dy}}{{dx}}{sin}\left(\frac{\pi}{\mathrm{180}}{x}\right)={cos}\left(\frac{\pi}{\mathrm{180}}{x}\right) \\ $$$$ \\ $$
